OPTIMIZACIÓN MATEMÁTICA MULTIOBJETIVO: UN PROCEDIMIENTO METAHEURÍSTICO INTELIGENTE APLICADO A LA SEGMENTACIÓN DE MERCADO EN UNA EMPRESA EMBOTELLADORA

Roger Z. Ríos Mercado*, M. Angélica Salazar-Aguilar*

CIENCIA UANL / AÑO 22, No.96 julio-agosto 2019

https://doi.org/10.29105/cienciauanl22.96-5

 

RESUMEN

En este trabajo se aborda un problema de diseño territorial motivado por una problemática real en el sector de repartición de bebidas embotelladas.  Éste es un problema de toma de decisiones donde debe decidirse cómo particionar el conjunto de manzanas geográficas de una ciudad en varios territorios para eficientar las tareas y el servicio proporcionado por la empresa a sus clientes.  El problema se plantea como una cuestión de optimización biobjetivo, donde se desea optimizar simultáneamente dos medidas de desempeño: la dispersión territorial y el desbalance territorial respecto a la demanda del producto. El problema está también sujeto a restricciones de balance con respecto al número de clientes y conectividad territorial.  Para resolver este complejo problema se ha desarrollado e implementado una metaheurística multiobjetivo basada en búsqueda dispersa.  Se presenta una evaluación computacional donde se demuestra el excelente desempeño del método propuesto, superando incluso a los mejores dos métodos conocidos a nivel mundial para problemas de optimización multiobjetivo (NSGA-II y SSPMO).

Palabras clave: investigación de operaciones, diseño de territorios, optimización multiobjetivo, metaheurísticas.

ABSTRACT

A territory design problem motivated by a real-world application in the bottled beverage distribution industry is addressed in the present research. The problem is categorized as a decision-making problem, where suitable partition of customers or city blocks in a city into territories must be decided, such that companies can provide a better service. The problem was modeled as a bi-objective optimization problem, where two performance responses are simultaneously optimized; (i) territory dispersion and (ii) territory imbalance with respect to product demand.  The problem is subject to balancing with respect to the number of customers and territory connectivity constraints.  To solve the complex problem, a scatter search-based multi-objective metaheuristic method has been developed and implemented.  An empirical assessment showed the performance of the proposed method, outperforming the two most popular methods used worldwide (NSGA-II and SSPMO).

Keywords: operations research, territory design, multi-objective optimization, metaheuristics.

En este trabajo se aborda un problema de diseño de territorios comerciales, el cual consiste en dividir un conjunto dado de unidades básicas (UBs) en p grupos llamados territorios, de acuerdo a algunos criterios específicos de planeación.  Se considera una versión biobjetivo del problema, es decir, se optimizan simultáneamente dos funciones objetivo. 

La versión monoobjetivo de este problema fue introducida por Ríos-Mercado y Fernández (2009). Debido a la complejidad del problema, ellos desarrollaron un procedimiento GRASP (Greedy Randomized Adaptive Search Procedure) reactivo para resolverlo. El procedimiento que propusieron superó el método utilizado en la compañía, tanto en la calidad de la solución como en el grado de infactibilidad con respecto a los requerimientos de balance. También se han estudiado diferentes versiones monoobjetivo de este problema (López-Pérez y Ríos-Mercado, 2013; Ríos-Mercado y López-Pérez, 2013; Ríos-Mercado y Escalante, 2016).

En relación a estudios multiobjetivo para otros problemas de distritos, hay algunas pocas aplicaciones, por ejemplo, en distritos políticos (Bong y Wang, 2004), distritos escolares (Bowerman, Hall y Calamai, et al., 1995) y servicios públicos (Tavares-Pereira et al., 2007). Sin embargo, éstos son modelos diferentes al que se estudia en este trabajo. Antes de realizar este proyecto, los únicos trabajos en diseño de territorios comerciales multiobjetivo eran los de Salazar-Aguilar et al. (2011a; 2013). En el primero, se introdujo el modelo biobjetivo y se propuso un método mejorado del ε-constraint para encontrar las fronteras óptimas de Pareto. Una de las limitaciones de este trabajo es, por supuesto, el tamaño de las instancias que podrían ser resueltas de forma exacta. La instancia más grande que se puede tratar con ese método tiene 150 UBs y seis territorios. En el segundo trabajo se desarrollaron heurísticas basadas en GRASP para tratar de abordar instancias de gran escala del problema, el desempeño de los métodos fue relativo. Por tanto, la motivación del  presente trabajo fue el de desarrollar un mejor método y más efectivo para abordar instancias grandes del problema de diseño de territorios comerciales (TDP, por sus siglas en inglés). Para mayor detalle acerca de otras aplicaciones de TDP mono-objetivo, el lector puede referirse al trabajo de Kalcsics y Ríos-Mercado (Kalcsics y Ríos-Mercado, 2019).

En este trabajo se desarrolló una metaheurística basada en búsqueda dispersa (SS). El método de búsqueda dispersa para diseño de territorios multiobjetivo (SSMTDP, por sus siglas en inglés) propuesto en este trabajo fue evaluado en un conjunto de instancias grandes. Los resultados indican que el SSMTDP es capaz de encontrar buenas soluciones que están muy bien distribuidas a lo largo de la frontera eficiente. Incluso si las soluciones iniciales tienen una evaluación pobre en las funciones objetivo, el método de combinación propuesto tiene la habilidad de explorar nuevas regiones en el espacio de búsqueda y el método mejorado permite obtener mejores soluciones que están bastante lejos del conjunto inicial. Cuando se comparó con el estado del arte de los métodos multiobjetivo como el procedimiento de búsqueda dispersa tabú para optimización multiobjetivo (SSPMO) y el algoritmo genético de clasificación no-dominada (NSGA-II), se encontró que estos procedimientos se esforzaron bastante para generar soluciones factibles del problema. Se observó que pocas instancias pueden ser resueltas con estos procedimientos. En contraste, el SSMTDP reportó soluciones significativamente mejores para aquellas instancias resueltas tanto por SSPMO como por NSGA-II.

DESCRIPCIÓN DEL PROBLEMA

Dado un conjunto V de manzanas (unidades básicas, UBs), la compañía desea dividir este conjunto en un número fijo (p) de territorios disjuntos satisfaciendo algunos criterios de planeación como balance, conexidad y compacidad. Se requiere el balance en los territorios para asegurar una mejor distribución de la carga de trabajo. La conexidad garantiza la movilidad dentro de los territorios, es decir que, cada territorio tiene que estar conectado de tal forma que se pueda llegar a cada unidad básica desde cualquier otra sin salir del territorio. La compacidad del territorio se requiere para garantizar que los clientes dentro del territorio estén relativamente cerca unos de otros. La compañía identifica a la compacidad y el balance respecto al número de clientes como los criterios más importantes. Por tanto, en el presente trabajo estos criterios son considerados como funciones objetivo y los criterios restantes se tratan como restricciones.

Sea G = (V,E), donde E es el conjunto de aristas que representan la adyacencia entre UBs. Una arista e ϵ E conectando a los nodos i y j existe si i y j son UBs adyacentes. A cada nodo j ϵ V se le asocian múltiples atributos como coordenadas geográficas (c_j^x, c_j^y), número de clientes y volumen de ventas. Específicamente, la compañía desea un balance perfecto entre los territorios, es decir, cada territorio debe contar con la misma cantidad de clientes y el mismo volumen de ventas. Sea K el conjunto de índices de territorios tal que |K|=p. Sea A = {1,2} el conjunto de actividades nodales, donde 1 es el número de clientes y 2 el volumen de ventas. Definimos el tamaño del territorio X_K con respecto a la actividad a como w^(a)(X_k) = ∑iϵX_Kw_i^(a), donde w_i^(a)  es el valor asociado a la actividad a ϵ A en el nodo i ϵ V. El valor promedio (deseado) está dado por µ^(a)= ∑iϵX_Kw_i^(a)/p. Debido a la naturaleza discreta de este problema, es prácticamente imposible tener territorios perfectamente balanceados. Por consiguiente, se introdujo un parámetro de tolerancia τ⁽²⁾ para el volumen de ventas que permite una desviación relativa con respecto al valor promedio µ⁽²⁾. Para medir la dispersión utilizamos la medida de dispersión del conocido problema de la p-mediana. Bajo los supuestos anteriores, el modelo combinatorio biobjetivo puede escribirse como:

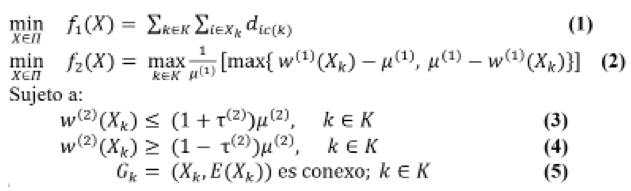
El objetivo es encontrar una p-partición X= (X₁ ,…, X_p) de V, tal que, tanto la dispersión (1) en cada territorio como la desviación máxima relativa con respecto al número de clientes en cada territorio (2) sean minimizados simultáneamente. Las restricciones (3)-(4) establecen que el tamaño del territorio (volumen de ventas) debe estar entre el rango permitido por el parámetro de tolerancia τ⁽²⁾. Las restricciones (5) aseguran la conexidad de cada territorio, donde G_k es el grafo inducido en G por el conjunto de nodos X_K. El problema anterior es NP-duro (Salazar- Salazar-Aguilar,  2011b).

PROCEDIMIENTO DE SOLUCIÓN PROPUESTO

El enfoque evolutivo llamado búsqueda dispersa (SS, por sus siglas en inglés) se basa en diversificar la búsqueda en el espacio de soluciones. Opera sobre un conjunto de soluciones denominado el conjunto de referencia, formado por soluciones buenas y diversas de la población principal. Éstas son combinadas con el propósito de generar nuevas soluciones con mejor valor objetivo, mientras se mantiene la diversidad. La estructura básica de SS (Martí, Laguna y Glover, 2006) está formada por cinco módulos principales. La figura 1 ilustra la representación esquemática del SS propuesto, donde se muestra cómo interactúan los módulos.

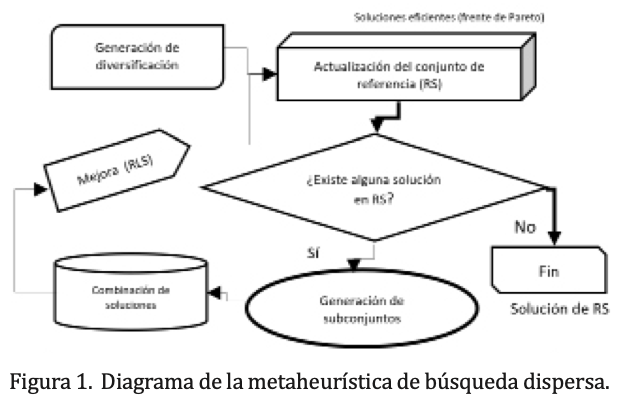
SS es una técnica muy flexible debido a que algunos módulos de su estructura pueden definirse de acuerdo al problema bajo estudio. Por ejemplo, en este trabajo, los módulos de diversificación, mejora y combinación se propusieron e implementaron ad hoc para este problema específico, para tratar de aprovechar su estructura. En nuestro diseño, el módulo de diversificación genera un conjunto de soluciones iniciales apoyado en estrategias de GRASP, en las cuales la función voraz está basada en las dos funciones objetivo del problema. El módulo de mejora trata de optimizar una solución dada utilizando una estrategia de búsqueda local encadenada para problemas multiobjetivo, utilizando las funciones objetivo del problema una a la vez de forma secuencial. El módulo de combinación de soluciones transforma dos soluciones dadas en una o más soluciones (hijos), tratando de mantener características buenas de las soluciones combinadas; el módulo de generación de subconjuntos genera las soluciones a ser combinadas en el módulo anterior. En esta aplicación específica se generan exactamente tres soluciones hijo de dos diseños de territorio dados. Estos tres módulos del problema específico se describen completamente en Salazar-Aguilar et al. (2012). Finalmente, los dos módulos restantes, los cuales no son dependientes del problema, son el módulo de actualización del conjunto referencia y el módulo de generación de conjuntos. El primero de los módulos mantiene una porción de las mejores soluciones en el conjunto referencia. En este caso, el conjunto referencia está formado por soluciones no-dominadas que van de acuerdo al criterio de Pareto, donde se consideraron ambas funciones objetivo del problema. Cuando se encuentra una solución no-dominada, ésta entra al conjunto de referencia y aquellas soluciones que son dominadas por la solución que se agregó son eliminadas del conjunto de referencia. El módulo de generación de subconjuntos actúa en el conjunto de referencia, en éste los subconjuntos de soluciones que deben ser combinados son creados por todos los pares de soluciones posibles del conjunto de referencia. 

Durante cada iteración del SSMTDP, se utilizó una memoria temporal para evitar combinaciones que fueron realizadas en la iteración previa. En otras palabras, para una iteración específica, el proceso de combinación se aplica sólo para aquellos pares de soluciones que no fueron combinados en la iteración anterior.

TRABAJO EXPERIMENTAL

El procedimiento fue programado en C++, y compilado en Sun C++ versión 8.0 bajo el sistema operativo Solaris 9, y se ejecutó en un SunFire V440. Los conjuntos de datos se tomaron de la base de datos (Ríos-Mercado y Fernández, 2009). Estos conjuntos de datos contienen instancias generadas aleatoriamente basadas en datos reales proporcionados por una compañía. El SSMTDP se aplicó sobre dos conjuntos de instancias con (n,p) ϵ  {(500,20),(1000,50)}. Para cada conjunto se generaron diez instancias y se utilizó un parámetro de tolerancia τ⁽²⁾ = 0.05 para todos ellos. Se utilizaron dos criterios de parada en el SSMTDP, límite de iteraciones y convergencia. En estos experimentos, el número máximo de iteraciones es 10.

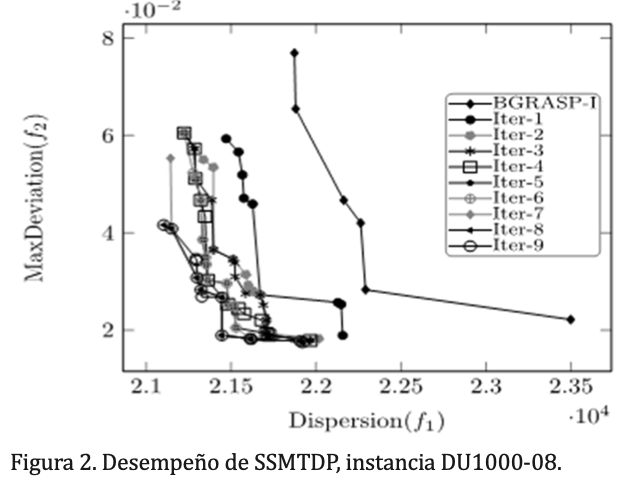
Durante el trabajo experimental, se observó que el SSMTDP convergió sin alcanzar el número máximo de iteraciones en todas las instancias probadas. Así, en todos los casos el SSMTDP se detuvo cuando no hubo nuevas soluciones para agregarse al conjunto de referencia. La figura 2 muestra el desempeño del SSMTDP para la instancia DU500-08, con 500 UBs y 20 territorios. La primera frontera (BGRASP-I) es el conjunto de soluciones iniciales generado por el módulo de diversificación (BGRASP-I). Las siguientes fronteras muestran las soluciones que pertenecen al conjunto de referencia en cada iteración del SSMTDP. Recuerde que el SSMTDP comienza con un conjunto de soluciones no-dominadas que se obtiene a través del módulo de diversificación. Estas soluciones se asignan al conjunto de referencia inicial. Después de eso, cada par de soluciones en el conjunto de referencia es combinado para generar tres soluciones diferentes. Las nuevas soluciones generadas son mejoradas a través del RLS y después se actualiza el conjunto de referencia obtenido, así se genera un nuevo conjunto de referencia. Cuando el conjunto de referencia ya no cambia, el SSMTDP se detiene. En el caso mostrado en la figura 2, el SSMTDP converge en la iteración 9. Es decir, en esta iteración, la combinación de las soluciones del conjunto de referencia no produjo soluciones no-dominadas para agregarse al conjunto de referencia. De esta manera, el SSMTDP reporta como conjunto de soluciones no-dominadas a aquéllas que pertenecen al conjunto de referencia en la última iteración.

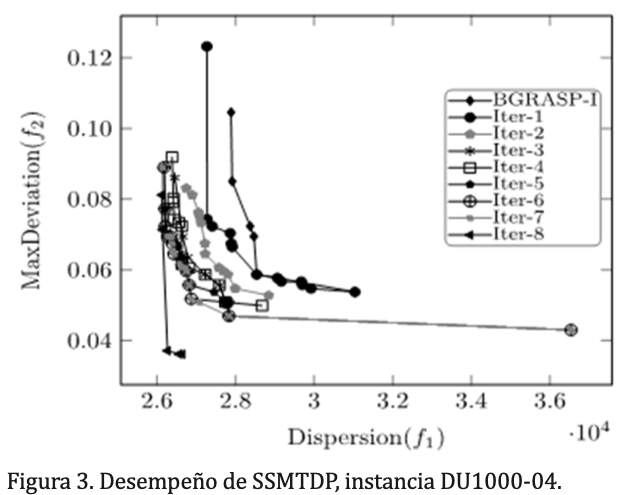
Para mostrar el comportamiento del SSMTDP utilizando instancias de tamaño (1000,50), la figura 3 muestra las iteraciones del SSMTDP para la instancia denominada DU1000-04, la cual tiene 1000 UBs y 50 territorios. En este caso, el SSMTDP se detuvo en la iteración 8. En resumen, las fronteras eficientes aproximadas obtenidas por el SSMTDP representan una mejora significativa con respecto a las fronteras iniciales obtenidas por el BGRASP-I. Se observó que en todas las instancias probadas (20 instancias), el método SSMTDP se detuvo por convergencia.

En las siguientes secciones se compara el SSMTDP con otras dos heurísticas del estado del arte, NSGA-II y SSPMO.  
Se han utilizado diferentes medidas de desempeño para evaluar la calidad de las soluciones obtenidas desde el enfoque multiobjetivo. Aquí consideramos las medidas más populares reportadas en la bibliografía de optimización multiobjetivo (Salazar-Aguilar et al., 2012): 
     1. Número de puntos en la frontera no-dominada. Es una medida importante ya que las fronteras no-dominadas que proveen más alternativas al tomador de decisiones son preferidas en lugar de aquéllas que contienen pocas. 
     2. k-distancia. Esta métrica es la distancia euclidiana desde un punto no-dominado al k-ésimo punto no-dominado más cercano. Debido a que la k-distancia está definida para un solo punto en la frontera, se consideran dos medidas en la evaluación de los resultados, específicamente, el promedio y los valores k-distancia máximos calculados sobre todos los puntos de la frontera obtenidos por el método. Por consiguiente, cuanto más pequeña es la k-distancia para los puntos en la frontera, la densidad de la frontera es mejor. En este trabajo se utiliza k=4. 
     3. Tamaño del espacio cubierto (SSC(X)). Para un conjunto de puntos dado X, SSC(X) es el volumen de los puntos dominados por X. Entonces, cuanto más grande es el valor de SSC(X), X es mejor. Específicamente, sea X = (X¹,…, X^k) un conjunto de k vectores de decisión. La función SSC(X) da el volumen incluido por la unión de los politopos P¹, …, P^k ,  donde cada  Pⁱ se forma por las intersecciones de los siguientes hiperplanos originados por Xⁱ, junto con los ejes: para cada eje en el espacio objetivo, existe un hiperplano perpendicular al eje y pasa a través del punto (?₁(X¹), …, ?_k(X^k)). En el caso de dos dimensiones, cada Pⁱ  representa un rectángulo definido por los puntos (0,0) y (?₁(X¹),  ?₂(X² ). Para evitar calcular volúmenes infinitos, el volumen calculado es dividido por el volumen de un hipercubo de referencia (ajustando tanto las cotas superiores como inferiores para cada objetivo) así el resultado final es mostrado en porcentaje. 
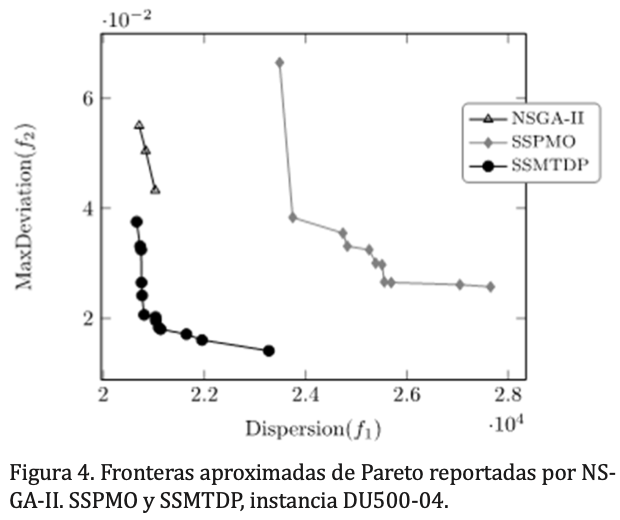
     4. C(A,B). Es conocido como la medida de cobertura de dos conjuntos. Esta medida representa la porción de puntos en la frontera eficiente B que son dominados por los puntos de la frontera A. Así, C(A,B) es la cobertura de B por puntos en A.

Comparación entre NSGA-II, SSPMO y SSMTDP

SSPMO es una metaheurística introducida por Molina et al. (2007) desarrollada inicialmente para resolver problemas de optimización no lineal multiobjetivo; sin embargo, también se ha adaptado para problemas combinatorios multiobjetivo. Éste consiste en un procedimiento de búsqueda dispersa/tabú híbrido que incluye dos diferentes fases: (i) generación de un conjunto inicial de puntos no-dominados a través de la búsqueda (MOAMP) local encadenada (tabú), y (ii) combinación de soluciones y actualización del conjunto no-dominado mediante búsqueda dispersa. 

El algoritmo genético de clasificación no-dominada (NSGA-II) es un algoritmo evolutivo que se ha aplicado con éxito a muchos problemas de optimización combinatoria multiobjetivo en la bibliografía (Deb et al., 2002), y es el método más citado en metaheurísticas multiobjetivo. Los detalles de cómo éstos fueron implementados en nuestro estudio  están en Salazar-Aguilar et al. (2012).

El NSGA-II se aplicó a los dos conjuntos de datos anteriormente descritos. El número de generaciones y el tamaño de la población se establecieron en 500. En cada generación se combinaron 250 soluciones. NSGA-II reportó soluciones no-dominadas sólo para la instancia DU500-04 (tablas I y II), la cual tiene 500 UBs y 20 territorios. Para las otras 19 instancias probadas, NSGA-II no brindó soluciones factibles, mientras que el procedimiento SSMTDP reportó soluciones no-dominadas para todas las instancias probadas. Se observó cómo NSGA-II falló en manejar apropiadamente las restricciones de conexidad. La mayoría de las soluciones generadas por NSGA-II son altamente infactibles respecto a las restricciones de conexidad, aun cuando NSGA-II considera este requerimiento como objetivo que debe ser minimizado. Los mecanismos de selección y los módulos de combinación no son suficientes para manejar estas restricciones difíciles. En contraste, el procedimiento propuesto SSMTDP está específicamente diseñado para tomar en cuenta la conexidad en todos sus componentes. Entonces, para este problema, aprovechar su estructura definitivamente vale la pena.  La figura 4 muestra la comparación entre los procedimientos SSMTDP, SSPMO y NSGA-II.

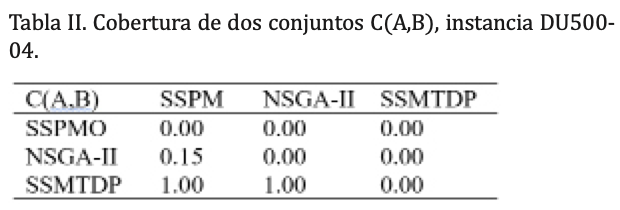
Observe que pocas soluciones no-dominadas de SSPMO son dominadas por el conjunto no-dominado reportado por NSGA-II. Además, tanto SSPMO como SSMTDP reportaron puntos no-dominados en una región que no está cubierta por la frontera de Pareto obtenida por NSGA-II.

La tabla I muestra nuevamente la superioridad de SSMTDP que claramente supera a NSGA-II y SSPMO, demostrando la eficiencia del método propuesto. Analizamos el caso particular (instancia DU500-04) en el cual NSGA-II reportó soluciones factibles. Note que en la k-distancia (media y max), los valores correspondientes para NSGA-II no pueden ser calculados dado que se utilizó k=4. La cobertura de dos conjuntos medida C(A,B) se muestra en la tabla II, en esta tabla el conjunto A se asocia con las filas y B con las columnas. Observe que los puntos obtenidos por NSGA-II dominaron algunos puntos obtenidos por SSPMO. La tabla II muestra que NSGA-II domina 15% de los puntos reportados por SSPMO. Para esta métrica, SSMTDP domina las fronteras reportadas por NSGA-II y SSPMO (vea figura 4). Además, NSGA-II reportó soluciones factibles sólo para una instancia de las 20 utilizadas, mientras que SSMTDP reportó soluciones factibles para todas las instancias. En resumen, SSMTDP supera a ambos procedimientos, NSGA-II y SSPMO.

CONCLUSIONES

En este trabajo se describe un procedimiento heurístico innovador basado en búsqueda dispersa para el problema biobjetivo de diseño territorial comercial. Cada componente del método propuesto llamado SSMTDP se diseñó tomando ventaja de la estructura del problema. En las pruebas computacionales, el método superó significativamente a los mejores métodos existentes (SSPMO y NSGA-II).  Desde la perspectiva práctica, el método es muy útil para asistir a los tomadores de decisiones, ya que al generar diversas soluciones no dominadas, éstas típicamente se discuten entre paneles de decisores donde se argumentan las preferencias por las diferentes funciones objetivo.  Al final, entre los decisores se propone una solución que representa el mejor compromiso.

AGRADECIMIENTOS

Este trabajo fue apoyado por el Conacyt (apoyos 48499-Y y 61903) y la UANL (Paicyt CE012-09). El segundo autor agradece la beca doctoral de la UANL (beca NL-2006-C09-32652).

* Universidad Autónoma de Nuevo León. 
Contacto: roger.rios@uanl.edu.mx

REFERENCIAS

Bong, C.W., y Wang, Y.C. (2004). A multiobjective hybrid metaheuristic approach for GIS-based spatial zone model. Journal of Mathematical Modelling and Algorithms. 3(3):245-261. 
Bowerman, R., Hall, B., y Calamai, P. (1995). A multi-objective optimization approach to urban school bus routing: Formulation and solution method. Transportation Research Part A. 29(2):107-123. 
Deb, K., Pratap, A., Agarwal, S., et al. (2002). A fast elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation. 6(2):182-197.  
Kalcsics, J., y Ríos-Mercado, R.Z. (2019a). Districting problems. En Location Science, 2a edición, Capítulo 25. Springer, Cham, Suiza. Aceptado. 
López-Pérez, J.F., y Ríos-Mercado, R.Z. (2013). Embotelladoras ARCA uses operations research to improve territory design plans. Interfaces. 43(3):209-220. 
Martí, R., Laguna, M., y Glover, F. (2006). Principles of scatter search. European Journal of Operational Research. 169(2):359-372. 
Molina, J., Martí, R., y Caballero, R. (2007). SSPMO: A scatter tabu search procedure for non-linear multiobjective optimization. INFORMS Journal on Computing. 19(1):91-100. 
Ríos-Mercado, R.Z., y Fernández, E. (2009). A reactive GRASP for a commercial territory design problem with multiple balancing requirements. Computers & Operations Research. 36(3):755-776. 
Ríos-Mercado, R.Z., y López-Pérez, J.F. (2013). Commercial territory design planning with realignment and disjoint assignment requirements. Omega. 41(3):525-535. 
Ríos-Mercado, R.Z., y Escalante, H.J. (2016). GRASP with path relinking for commercial districting. Expert Systems with Applications. 44:102-113. 
Salazar-Aguilar, M.A., Ríos-Mercado, R.Z., y González-Velarde, J.L. (2011a). A bi-objective programming model for designing compact and balanced territories in commercial districting. Transportation Research Part C: Emerging Technologies. 19(5):885-895. 
Salazar-Aguilar, M.A., Ríos-Mercado, R.Z., y Cabrera-Ríos, M. (2011b). New models for commercial territory design. Networks & Spatial Economics. 11(3):487-507. 
Salazar-Aguilar, M.A., Ríos-Mercado, R.Z., González-Velarde, J.L., et al. (2012). Multiobjective scatter search for a commercial territory design problem. Annals of Operations Reseach. 199(1):343-360. 
Salazar-Aguilar, M.A., Ríos-Mercado, R.Z., y González-Velarde, J.L. (2013). GRASP strategies for a bi-objective commercial territory design problem. Journal of Heuristics. 19(2):179-200.  
Tavares-Pereira, F., Figueira, J.R., Roy, B., et al. (2007). Multiple criteria districting problems: The public transportation network pricing system of the Paris region. Annals of Operations Research. 154(1):69-92. 

RECIBIDO: 20/04/2018
ACEPTADO: 29/06/2019