El poder predictivo de la Teoría de la Relatividad General

Hernando Quevedo*
CIENCIA UANL / AÑO 20, No. 85, julio-septiembre 2017
Hace más de 100 años que en su Relatividad General, Einstein incluyó el versátil concepto de espaciotiempo con cuatro dimensiones. Para introducir en él la geometría diferencial se parte del concepto de distancia. Tomemos un evento arbitrario xμ que denotaremos mediante sus cuatro coordenadas xμ=(x1,x2,x3,x4 ). Empleamos aquí la notación x1,x2, etc., en lugar de las coordenadas cartesianas, para enfatizar el hecho de que se trata de coordenadas de sistemas no inerciales, en general. Consideremos un segundo evento con coordenadas xμ+dxμ, donde xμ<<dxμ, es decir, el segundo evento se encuentra muy cerca del primero. En la Figura 1 se ilustra esta situación, donde el espaciotiempo está representado esquemáticamente como una superficie curva bidimensional.
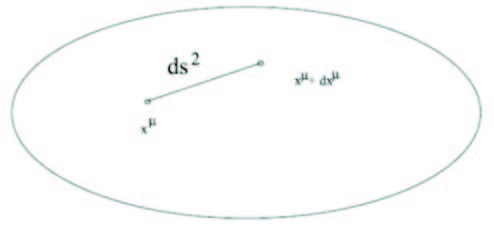
Figura 1. Dos eventos en el espaciotiempo separados por una distancia
infinitesimal.
En geometría diferencial, la distancia o elemento de línea ds2 entre los dos eventos definidos anteriormente se define como
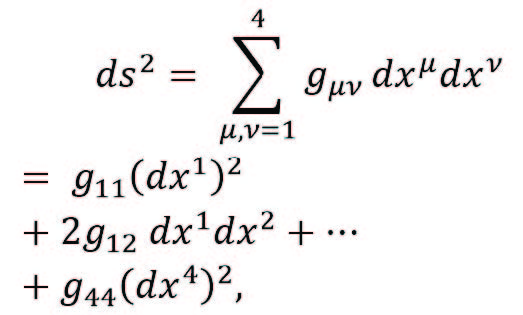
(1)
donde gμν es una matriz simétrica 4×4 que depende de cada espaciotiempo en particular. En geometría diferencial esta matriz lleva el nombre de métrica. En calidad de ejemplo, consideremos el elemento de línea del espaciotiempo de Minkowski, el cual es usado en relatividad especial y corresponde a la convención xμ=(ct,x,y,z),
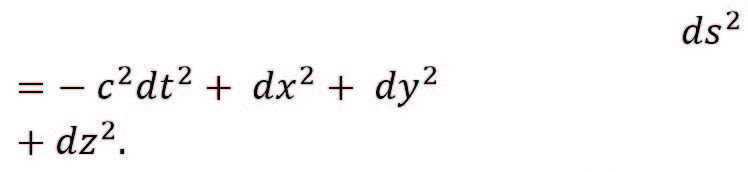
(2)
Se puede concluir inmediatamente que la métrica de Minkowski es diagonal y tiene la forma
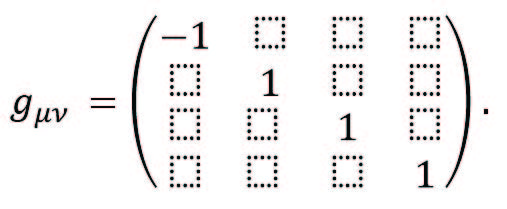
(3)
Para un espaciotiempo arbitrario las componentes de la métrica en general son funciones de las coordenadas. En geometría diferencial, con el tipo que se utiliza en relatividad general se puede demostrar que toda la información geométrica del espaciotiempo se encuentra codificada en la métrica.
Una magnitud muy importante de cualquier espaciotiempo que se deriva de la métrica es la curvatura o, siendo más exactos, el tensor de curvatura de Riemann. Se puede demostrar que la curvatura depende de las primeras y segundas derivadas de la métrica con respecto a las coordenadas. Veamos el caso sencillo de la métrica de Minkowski (3). Puesto que todas las componentes de la métrica son constantes, sus primeras y segundas derivadas son cero y, por lo mismo, se puede demostrar que la curvatura es cero. Decimos entonces que el espaciotiempo de Minkowski es plano. De hecho, se puede demostrar que el único espaciotiempo plano es el de Minkowski, teniendo como consecuencia que la relatividad especial corresponde a una geometría plana.
En el caso de relatividad general, como ya mencionamos, la métrica depende de las coordenadas y por lo tanto sus derivadas son diferentes de cero y pueden llevar a curvaturas diferentes de cero. De hecho, se puede demostrar que cuando la curvatura es diferente de cero, el espaciotiempo correspondiente forma parte de la relatividad general y puede llegar a tener un sentido físico específico.
Por otra parte, vimos que de acuerdo al principio de equivalencia débil no es posible distinguir locamente entre un sistema de referencia acelerado y un campo gravitacional. Esto llevó a Einstein a conjeturar uno de los conceptos más importantes de física teórica, a saber:
Curvatura del espaciotiempo ≡ fuerza gravitacional
El signo de equivalencia significa que para conocer la fuerza gravitacional es suficiente con medir la curvatura del espaciotiempo y viceversa. Por ende, si un espaciotiempo es curvo, existe un campo gravitacional que genera la curvatura.
Para determinar en cada caso concreto la relació entre la curvatura del espaciotiempo y el campo gravitacional correspondiente, se utilizan las ecuaciones de Einstein que se escriben de la siguiente manera:
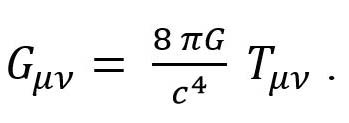
(4)
Aquí Gμν es el tensor de Einstein que depende de la métrica gμν y de sus primeras y segundas derivadas con respecto a las coordenadas del espaciotiempo. El tensor de Einstein contiene solamente magnitudes geométricas y su cálculo explícito se obtiene a partir de la curvatura del espaciotiempo. La parte derecha de las ecuaciones (4) contiene el tensor de energía-momento Tμν que depende directamente de magnitudes físicas como la masa, presión, volumen, etc. Consecuentemente, las ecuaciones de Einstein tienen un sentido físico muy profundo ya que se pueden interpretar conceptualmente como
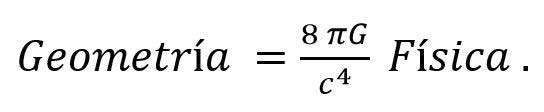
(5)
La constante de proporcionalidad ![]() contiene la velocidad de la luz en el vacío c y la constante gravitacional de Newton G, de forma tal que nos permite relacionar la magnitud geométrica curvatura con magnitudes físicas como la energía, presión, etc. Esta equivalencia entre magnitudes geométricas fue propuesta por primera vez por Einstein para el campo gravitacional, pero hoy en día sabemos que es válida para todos los demás campos conocidos en la naturaleza.
contiene la velocidad de la luz en el vacío c y la constante gravitacional de Newton G, de forma tal que nos permite relacionar la magnitud geométrica curvatura con magnitudes físicas como la energía, presión, etc. Esta equivalencia entre magnitudes geométricas fue propuesta por primera vez por Einstein para el campo gravitacional, pero hoy en día sabemos que es válida para todos los demás campos conocidos en la naturaleza.
Técnicamente, las ecuaciones de Einstein (4) corresponden
a diez ecuaciones diferenciales de segundo orden para la métrica gμν. En principio, cada una de sus soluciones debería describir el campo gravitacional de alguna distribución de masa descrita por algún tensor energía-momento Tμν. Hoy se conocen muchas soluciones
exactas a estas ecuaciones, pero no a todas se les ha podido encontrar su sentido físico. Veamos unos pocos ejemplos de importancia.
Supongamos que nos encontramos en el cosmos a cierta distancia r del centro de la Tierra y asumimos esta última como una esfera sin rotación. Si nos preguntamos cuál es la métrica que describe el campo gravitacional en ese punto, las ecuaciones de Einstein proporcionan la respuesta en forma del elemento de línea de Schwarzschild:
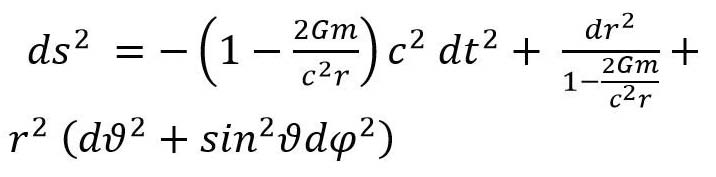
(6)
en coordenadas esféricas xμ=(t,r,ϑ,φ).
En esta métrica aparece el parámetro m que es el valor de la masa de la Tierra. Los experimentos indican que esta métrica describe con buena exactitud el campo gravitacional de la Tierra fuera de su atmósfera. Con esta métrica se pueden a su vez determinar las trayectorias de objetos pequeños como satélites artificiales alrededor de la Tierra. Las predicciones de la teoría de la relatividad concuerdan muy bien con los datos observacionales.
Otro ejemplo de solución a las ecuaciones de Einstein está dado mediante el elemento de línea de Friedmann-Lemaitre-Robertson-Walker que se puede representar en coordenadas esféricas como
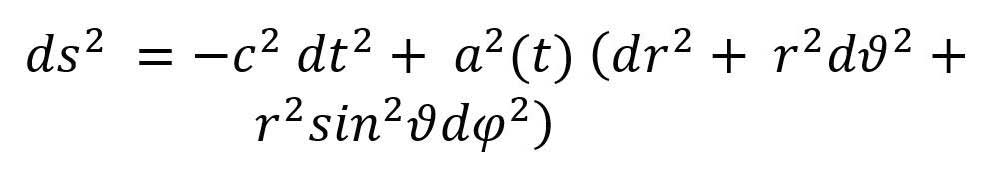
(7)
donde la función a(t) debe satisfacer las ecuaciones de Einstein que en este caso se reducen a:
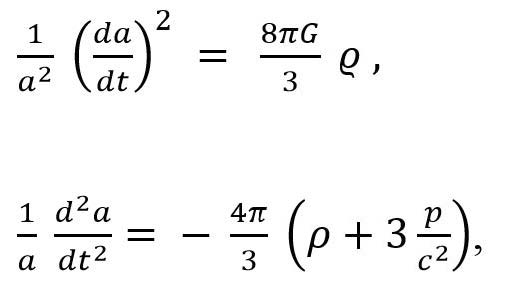
(8) y (9)
donde ϱ=ϱ(t) es la densidad de energía y p=p(t) es la presión. Si ahora asumimos que nuestro universo se puede describir como un fluido de energía ϱ(t) y presión p(t), magnitudes físicas que podemos determinar con base en las observaciones cosmológicas, la teoría de Einstein predice que la métrica (25) junto con las ecuaciones (26) y (27) describen la evolución del Universo. Las observaciones muestran que esta predicción es correcta.
Otra solución a las ecuaciones de Einstein predice la existencia de ondas gravitacionales a través de una métrica que es un tanto más compleja para ser incluida en esta breve descripción. La existencia de estas ondas fue corroborada apenas en 2015, más de cien años después de su predicción.
Los ejemplos mencionados anteriormente muestran la gran capacidad de predicción que tiene la relatividad general como una teoría que describe el campo gravitacional. Aún existen muchos problemas por resolver en la teoría de la relatividad y es por eso que en la mayoría de las grandes universidades del mundo se llevan a cabo investigaciones de índole teórica y experimental.
A los lectores interesados en profundizar sus conocimientos de la teoría de la relatividad a nivel conceptual y técnico se les recomiendan los libros de texto incluidos en las referencias.

Figura 2. El anillo de Einstein. Imagen generada por computadora a partir de distorsiones causadas por un hoyo negro esféricamente simétrico y sin carga (Alain Riazuelo, IAP/UPMC/CNRS, http://www2.iap.fr/users/riazuelo/bh/APOD.php).
*Universidad Nacional Autónoma de México
Contacto: quevedo@nucleares.unam.mx
Referencias
Misner, C., Thorne, K., y Wheeler, J. (1973). Gravitation. W. H. Freeman and Company, USA.
Schutz B. (2009). A first course in general relativity Cambridge University Press, UK.
