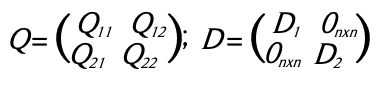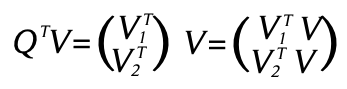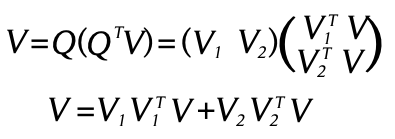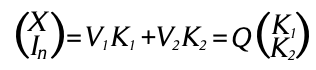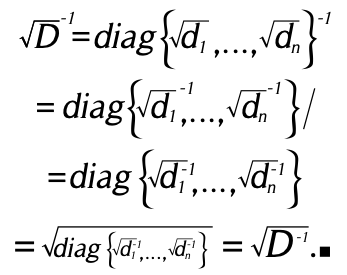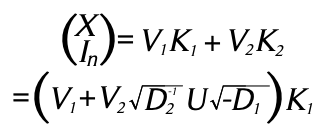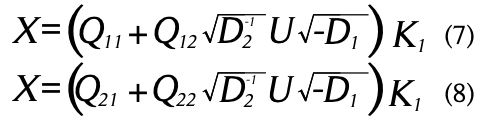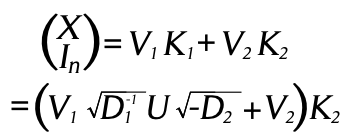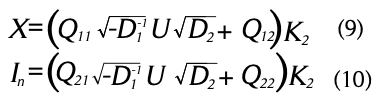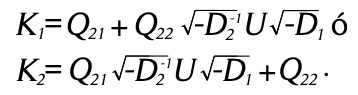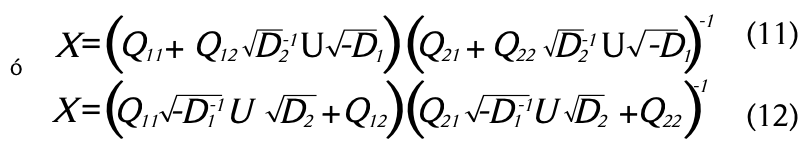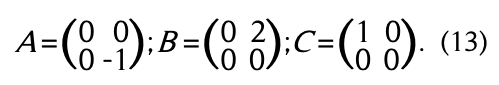Solución de la ecuación algebraica de Riccati
María Aracelia Alcorta-García* ORCID: 0000-0002-9079-27
Juan Carlos Hernández-Medellín* ORCID: 0000-0002-5191-9514
CIENCIA UANL / AÑO 27, No.127, septiembre-octubre 2024
DOI: https://doi.org/10.29105/cienciauanl27.127-5
RESUMEN
En este trabajo se obtiene un conjunto de soluciones para la ecuación algebraica de Riccati (ARE), la cual es expresada en términos de los coeficientes de la ecuación original sin necesidad de conocer una de las soluciones para, a partir de ésta, obtener la segunda, como se hace en el caso de la ecuación de Bernoulli. Las soluciones son obtenidas partiendo de una matriz simétrica S por bloques, formada con los coeficientes de la ARE. Las soluciones de la ARE son obtenidas partiendo del cálculo de los valores propios de S y aplicando los principios de ortogonalidad en una base de un módulo sobre el anillo 
. Este procedimiento supone condiciones de simetría en los coeficientes de la ARE y se considera que la diagonalización de la matriz por bloques S siempre es posible. La metodología propuesta se muestra en dos ejemplos.
Palabras clave: ecuación algebraica de Riccati, matriz por bloques, valores propios, vectores propios, diagonalización.
ABSTRACT
In this work, a set of solutions for the algebraic Riccati equation (ARE) is obtained, which is expressed in terms of the coefficients of the original equation without the need to know one of the solutions in order to obtain the second one, as it is done in the case or fthe Bernoulli equation. The solutions are obtained starting from a symmetric matrix S, by blocks, formed with the coefficients of the ARE. The solutions of the ARE are obtained by calculating the eigenvalues of S and applying the principles of orthogonality on the basis of a module over the ringR_(nxn). This procedure assumes symmetry conditions in the coefficients fo the ARE, and it is considered that the diagonalization of the block matrix S is always possible. Two examples are presented illustrating the proposed methodology.
Keywords: Algebraic Riccati equation, block matrix, eigenvalues, eigenvectors, diagonalization
La ecuación diferencial ordinaria dada por
donde P, Q y R son matrices cuyos elementos pueden ser funciones de x (o constantes), es llamada ecuación diferencial ordinaria de Riccati (EDOR), en honor al matemático italiano Jacopo Francesco Riccati, nacido en Venecia, República de Venecia, el 28 de mayo de 1676, y falleció en Treviso, Italia, el 15 de abril de 1754.
J.F. Riccati llegó a esta ecuación al analizar la hidrodinámica. En 1724 publicó una investigación multilateral de la ecuación, llamada, por iniciativa de D’Alembert (1769): Ecuación de Riccati. Algunos contemporáneos la analizaron, entre ellos Gottfried Wilhelm von Leibniz, matemático y filósofo alemán; Christian Goldbach, matemático originario de Kaliningrado, Rusia; Johann Bernoulli, matemático, médico y filólogo suizo, y sus hijos Nicolás y Daniel Bernoulli y, posteriormente, el matemático y físico suizo Leonhard Euler. Su trabajo se limitó al análisis de casos particulares de la ecuación.
Siendo ésta planteada y analizada en la forma que conocemos en los libros de texto (Dennis, 2012; Boyce, 2012) por la familia Bernoulli.
En algunas de las investigaciones se planteó la ecuación especial de Riccati, que sí posee solución en términos finitos en un número limitado de casos, para lo cual se requiere conocer una de las soluciones. Algunos trabajos han presentado soluciones de la ARE (Zoran, 2017), los autores usan un método recursivo de reducción de orden. Ai-Guo Wu, Hui-Jie Sun y Ying Zhang (2020) plantean la solución utilizando dos métodos de iteraciones.
La solución con restricciones más específicas, cuando se trata de un sistema hermitiano estabilizable, se puede ver en Zhang et al. (2024). La solución de la ecuación de Riccati no simétrica es planteada por Akbar Shirilord y Mehdi Dehghan (2022). La ecuación de Riccati parametrizada es presentada en Rojas (2021). Nguyen y Gajic (2010) presentan una solución de la ecuación diferencial matricial de Riccati, en este trabajo los autores emplean la solución definida antiestabilizante de la ARE y la solución de la ecuación diferencial matricial de Lyapunov. Hench et al. (1998) resuelven una ARE amortiguada y una ecuación degenerada de Riccati obtenida partiendo del problema de los controladores amortiguados.
Carpanese (2000) obtiene una solución de la ecuación en diferencias de Riccati (caso discreto). Adam (2000) verifica la continuidad de la solución de la ecuación diferencial de Riccati (EDR) y la ARE en el caso continuo en el tiempo. Un algoritmo para la solución de sistemas no triviales acoplados de ARE que aparecen en el problema de control Risk-sensitive es presentado por Freiling, Lee y Jank (1998), quienes usan métodos de comparación al obtener condiciones adecuadas de acotación en las soluciones de un problema de valor terminal en los sistemas de EDR acoplados.
Barabanov y Ortega (2004) presentan extensiones ocultas del lema Kalman-Yakubovich-Po- pov, referente a las condiciones de la solución en la matriz Lur’e-Riccati. Con Jiménez (2015) la EDR se resuelve en una ecuación diferencial de segundo orden, reduciéndola a una ecuación de Riccati, siempre y cuando los coeficientes en la ecuación diferencial estén relacionados de una forma específica, resolviendo posteriormente la ecuación de Riccati sin requerir el conocimiento de una de las soluciones. Una aproximación eficiente en la reso- lución de la EDR usando derivadas de orden fraccional se presenta en Alam, Ara y Jamil (2011). Cai, Ding y Li (2017) presentan una aplicación de la ecuación de Riccati en el problema de estimación. La continuidad de la solución de la ecuación de Riccati es presentada por Adam (2000).
El objetivo de este trabajo es establecer una metodología que facilite la obtención de la solución de la ARE, sin necesidad de conocer una de las soluciones, considerando los puntos de equilibrio propios del sistema.
Por otro lado, como una aplicación importante, por su participación en el problema de control (donde toma el rol de ecuación de ganancia del control) y programación dinámica (así se puede ver en Reid (1972), Petkov y Konstantinov (1991), Nguyen y Gajic (2010), entre otras publicaciones), retoma importancia el cálculo de los puntos de equilibrio de la misma y su solución, encontrándola asintóticamente estable en los puntos de equilibrio de la misma, logrando así un control eficiente.
Entre las propiedades de la EDOR que facilitan la existencia y obtención de las ecuaciones de control se encuentran la existencia de solución única para condiciones iniciales dadas y condicionando a que la EDOR sea definida positiva se llega al ajuste de la ecuación de control. El trabajo es organizado en la siguiente forma: sección 2 se presenta el planteamiento del problema, en la sección 3 se encuentra la solución de la ARE, y en la sección 4 se presentan dos ejemplos.
PLANTEAMIENTO DEL PROBLEMA
La EDR matricial en tiempo continuo, con solución 
está dada por
donde A, B, 
son matrices invariables en el tiempo, A y C son matrices simétricas. Los puntos de equilibrio para la EDR (1), son las soluciones de la ARE, que toma la forma:
donde 
Partiendo de la ARE (2), se forma la matriz a bloques simétrica (Jiménez, 2015) de dimensión 2nX2n, S:
Entonces la ARE (2) se puede representar de la siguiente manera:
Donde 
es la matriz identidad n×n.
Dado que S es simétrica, es diagonalizable ortogonalmente en R, esto implica que existe una matriz 
ortogonal y una matriz 
diagonal tal que S= QDQτ, como lo plantea Jiménez (2015). Las matrices Q y D pueden ser separadas en bloques tamaño n×n en la siguiente forma:
Dado que D es diagonal, entonces D1 y D2 también lo son. Tomando en cuenta lo anterior es establecido el siguiente lema.
Lema 1
Sean 
tales que 
Donde 
son matrices de dimensión 2nx2n.
Entonces, las siguientes igualdades se cumplen
Demosatración
Partiendo de la definición de 
De la diagonalización de S,D = QτSQ.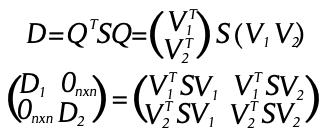
Entonces
Los resultados se obtienen de la igualdad de matrices anterior.
El lema 1 establece una estructura para matrices de dimensión 2n×n similar en los vectores
22 conjugados en R². Los vectores conjugados en R² son linealmente independientes y además forman una base de R². Sin embargo, en esta estructura, la “independencia lineal” tiene además las características dadas por la estructura de módulo sobre un anillo, lo cual se explica en el lema 2.
Lema 2. Estructura de módulo
Sean 
definidos como en el lema 1, éstos forman una base en 
en una especie de módulo derecho sobre el anillo de matrices .
Esto implica:
i. Para cada 
existen 
tales que 
ii. 
Demostración
i. Considere el producto
El cual siempre existe ya que Q es ortogonal.
Si 
que siempre existe, se llega al resultado i.
ii. La demostración de la suficiencia es trivial. Al probar la necesidad, considere 
y sustituyendo las expresiones para 
de la demostración de la parte i, se llega a ii.
Partiendo de lo planteado en el lema 2, toda matriz 2n×n puede ser escrita como una combinación módulo de . Esta matriz incluye la solución matricial de la ARE (2).
SOLUCIÓN DE LA ARE
Además existen tales que
Sustituyendo en (3), se obtiene: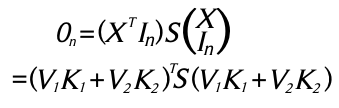
Haciendo las operaciones se llega a
Usando el lema 1, la expresión anterior se simplifica a: 
Esta ecuación puede ser escrita como
Para satisfacer esta ecuación, son necesarias las siguientes definiciones.
Definición 1. Raíz cuadrada de una matriz simétrica
Dada una matriz simétrica 
su raíz cuadrada es aluna matriz 
tal que 
Ésta es denotada por 
Definición 2. Raíz cuadrada principal
Dada una matriz diagonal 
con entradas no negativas, su raíz cuadrada principal es 
donde los elementos de su diagonal son la raíz cuadrada de los elementos de la matriz D.
Proposición 1
La raíz cuadrada de una matriz no es única. Si B es una raíz cuadrada de A, entonces UB, donde 
es ortogonal, es además una raíz cuadrada de A.
Demostración
Dado que 
Entonces 
Proposición 2
Sean M, 
y N simétrica. Entonces √NM es una raíz cuadrada de MτNM.
Demostración
Aplicando la proposición 2 en (5), es posible escribir
se obtiene
Proposición 3
Si D es una matriz diagonal no singular, con entradas positivas, entonces √D es también no singular y 
Demostración
. Dado que D es invertible, 
Esto implica que √
por lo tanto √D es invertible.
Además
Hasta aquí es posible resolver para 
en (6). Por otro lado, si 
es invertible, entonces
Con lo cual
Partiendo de las definiciones de en el lema 1, sustituyendo los resultados anteriores, tenemos:
Si 
es invertible, entonces
donde 
ha sido sustituida por U, ya que U es una matriz ortogonal arbitraria. Entonces
De donde se obtiene:
Para las ecuaciones (8) y (10) se tiene una solución en 
esto es
Éstas deben de ser invertibles ya que son factores de un producto que genera la matriz identidad. Por lo que su determinante no puede ser cero. El resultado anterior nos permite enunciar el siguiente teorema que presenta la solución de la ARE.
Teorema 1. Soluciones de la ARE
Sea la ARE definida como previamente, y sean Q y D las matrices de dimensión 2n×2n de la descomposición en valores propios de la matriz coeficiente particionada en n×n bloques. Entonces las soluciones de la CARE, parametrizadas con una matriz ortogonal 
tienen la forma
Siempre y cuando sea posible calcular las matrices inversas en las expresiones anteriores.
Demostración
Sustituyendo las expresiones en las ecuaciones (7) y (9) se obtiene el resultado.
Para éstas, la matriz S toma la forma
que tiene la siguiente descomposición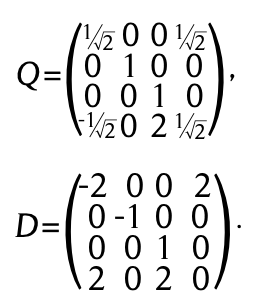
Usando la edición (11), y tomando la matriz ortogonal U como la matriz identidad 
se obtiene la solución:
Note que, en este caso, la matriz no es invertible, por lo tanto la ecuación (12) no puede ser usada.
*Universidad Autónoma de Nuevo León, San Nicolás delos Garza, México.
Contacto: maria.alcortagr@uanl.edu.mx
REFERENCIAS
Adam, C. (2000). Continuity of the solution of the Riccati equations for continuous time JLQP, IEEE Transactions on Automatic Control, 45(5), 934-937.
Alam, K.N., Ara, A., y Jamil, M. (2011). An efficient approach for solving the Riccati equation with fractional orders, in Elsevier (ed.), Computers & Mathematics with Applications, Elsevier, 2683-2689.
Barabanov, N.E., y Ortega R. (2004). On the solvability of extended Riccati equations, IEEE Transactions on Automatic Control, 49(4), 598-602.
Boyce, W.E., DiPrima, R.C. (2012). Elementary Differential Equations and Boundary Value Problems, John Wiley & Sons.
Cai, X., Ding, Y. S., y Li, S.Y. (2017). Convergent properties of Riccati equation with application to stability analysis of state estimation, Hindawi Athematical Problems in Engineering, 2017, 1-7.
Carpanese, N. (2000). Periodic Riccati difference equations: Approaching equilibria by implicit systems, IEEE Transactions on Automatic Control, 45(7), 1391-1396.
Dennis, G., y Wright, Zill. (2012). Elementary Differential Equations and Boundary Value Problems, John Wiley & Sons.
Freiling, G., Lee, S.R., y Jank, G. (1998). Coupled Matrix Riccati Equations in Minimal Cost Variance Control Problems, IEEE Transactions on Automatic Control, 4(3), 556-560.
Hench, J.J., He, C., Kvucera, V., et al. (1998). Coupled matrix Riccati equations in minimal cost variance control problems, IEEE Transactions on Automatic Control, 44(3), 556-560.
Jiménez, J.A. (2015). La solución de algunas EDO de Riccati, Revista Digital Matemática, Educación e Internet, 15(2).
Nguyen, T., y Gajic, Z. (2010). Solving the matrix differential Riccati equation: A Lyapunov equation approach, IEEE Transactions on Automatic Control, 55(1), 191-194. https://doi.org/10.1109/TAC.2009.2033841
Petkov, P., Christov, N., y Konstantinov, M. (1991). Computational Methods for Linear Control Systems, Prentice, New York.
Rojas, A.J. (2021). Modified Algebraic Riccati Equation Closed-Form Stabilizing Solution, IEEE Access, 9, 140667-140675. https://doi.org/10.1109/ ACCESS.2021.3119592.
Reid, W.T. (1972). Riccati differential equations, Academic Press.
Shirilord, Akbar, Dehghan, Mehdi, (2022). Closed-form solution of non-symmetric algebraic Riccati matrix equation, Applied Mathematics Letters, 131, https://doi.org/10.1016/j.aml.2022.108040
Wu, Ai-Guo, Sun, Hui-Jie, Zhang, Ying, (2020). A novel iterative algorithm for solving coupled Riccati equations, Applied Mathematics and Computation, 364, https://doi.org/10.1016/j.amc.2019.124645
Zhang, L., Chen, M.Z.Q., Gao, Z., et al. (2024). On the explicit Hermitian solutions of the continuous-time algebraic Riccati matrix equation for controllable systems, IET Control Theory Appl, 1-12, https://doi.org/10.1049/cth2.12618
Zoran, Gajic, Djordjija, Petkovski, Xuemin, Shen. (2017). Singularly perturbed and weakly coupled linear control systems, a recursive approach, Technical report, Springer Nature Switzerland AG.
Recibido: 17/10/2022
Aceptado: 07/03/2024