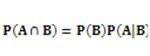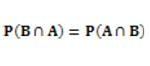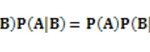Tema 34: El Teorema de Bayes
Peter B. Mandeville*
[W]hen people thought the earth was flat, they were wrong.
When people thought the earth was spherical, they were wrong.
But if you think that thinking the earth
is spherical is just as wrong as thinking the earth is flat,
then your view is wronger than both of them put together.
Isaac Asimov(1)
CIENCIA UANL / AÑO 16, No. 64, OCTUBRE-DICIEMBRE 2013
Las probabilidades simples, conjuntas y condicionales
Sean A y B dos eventos asociados con un experimento, ε. Sea n el tamaño de la muestra, n(A) el número de puntos con característica A, y n(B) el número de puntos con característica B, entonces las probabilidades simples de Ay B son: (2-13)
La probabilidad que ambos eventos sucedan es la probabilidad conjunta que es: (2-13)
La probabilidad de condicional del evento B, dado que el evento A ha sucedido es
que se relacionen las probabilidades simples, conjuntas y condicionales. 
representa la proporción de los n puntos con característica A, que también tienen característica B. Cada vez que se calculase calcula P(B) con respecto al espacio reducido de A en lugar del espacio original. (2-13)
El Teorema de Bayes
El Teorema de Bayes fue desarrollado por el reverendo Thomas Bayes en Essay towards solving a problem in the doctrine of chances, que fue publicado por la Royal Society of London en 1763, dos años después de su fallecimiento.(14)
Hubo poco interés en las ideas de Bayes hasta que fueron redescubiertas independientemente por Pierre-Simon, marqués de Laplace, quien publicó la formulación moderna en su Théorie analytique des probabilities (1812). (14)
Se supone que la causa A sucede antes del resultado B. De la definición de la probabilidad condicional se obtiene
lo que equivale a
y dado que
entonces
Las ecuaciones están relacionadas por el Teorema de Bayes
Entonces, dado un resultado, B puede calcular la probabilidad de la causa, A: (2-13)
El problema es que hay pocas veces que se conoce P(B).
El Teorema de la Probabilidad Total
Sea B algún evento con respecto a S y sea de A1, A2,…,Ak de una partición de S. Se supone que los eventos 
se excluyen mutuamente, por lo tanto, se puede aplicar la Regla de Adición y escribir
y
Dada la definición de la probabilidad condicional, se puede expresar cada término
como
y por tanto se obtiene el Teorema de la probabilidad total: (2-13)
Por el Teorema de la probabilidad total se puede escribir el Teorema de Bayes
Aplicación
Se puede utilizar la siguiente función en R15 para solucionar problemas que requiere el Teorema de Bayes:
Bayes <- function(e,p,pse){
cat(“\n Bayes Theorem\n\n”)
joint <- p*pse
ps <- sum(joint)
bayes <-
round(cbind(p,pse,joint,joint/ps),4)
colnames(bayes) <-
c(“P(E)”,“P(S|E)”,“P(E)P(S|E)”,“P(E|S)”)
rownames(bayes) <- c(e)
print(bayes)
cat(“\nP(S):”,round(ps,4),“\n”)
}
Los historiales médicos indican que muchas condiciones distintas pueden producir síntomas idénticos. Suponga que un conjunto particular de síntomas, al cual se denota como el suceso H, ocurre solamente con base en una de las tres condiciones A, B o C. Para simplificar, suponga que las condiciones A, B y C son mutuamente excluyentes. Ciertos estudios muestran que las probabilidades de contraer las tres condiciones son:
P(A) = 0.01
P(B) = 0.005
P(C) = 0.02
Las probabilidades de desarrollar los síntomas H, dada una condición específica, son:
P(H|A) = 0.90
P(H|B) = 0.95
P(H|C) = 0.75
Suponiendo que una paciente tiene los síntomas H,
> evento <- c(“A”,“B”,“C”)
> probabilidad <- c(0.01,0.005,0.02)
> condicional <- c(0.9,0.95,0.75)
>
Bayes(evento,probabilidad,condicional)
Bayes Theorem
– P(E) P(S|E) P(E) P(S|E) P(E|S)
A. 0.010 0.90 0.0090 0.3130
B. 0.005 0.95 0.0048 0.1652
C. 0.020 0.75 0.0150 0.5217
P(S): 0.0288
¿Cuál es la probabilidad de que tenga la condición A?
P(B|H) = 0.3130
¿Cuál es la probabilidad de que tenga la condición B?
P(B|H) = 0.1652
¿Cuál es la probabilidad de que tenga la condición C?
P(C|H) = 0.5217
¿Cuál es la probabilidad de los síntomas H?
P(H) = 0.0288
Se recomienda el texto de Bertsch McGrayne (14) para una fascinante revisión de la importancia del Teorema de Bayes.
*Consultor Asociado, BioEstadística, S.C.
(www.bioestadistica.com)
Contacto: peter.mandeville@bioestadistica.com
Referencias
1. Isaac Asimov. The Relativity of Wrong. The Skeptical Inquirer, 14(1), 35-44. Fall 1989.
2. Kenneth Baclawski. Introduction to Probability with R. Texts in Statistical Science. Chapman & Hall/CRC, Boca Raton, FL, USA. 2008.
3. Jay L. Devore. Probability and Statistics for Engineering and the Sciences. Fifth edition. Duxbury, Pacific Groove, CA, USA. 2000.
4. William Feller. Introducción a la teoría de probabilidades sus aplicaciones, volumen I. Editorial Limusa, S.A., México 1, D.F., México, 1983.
5. Brian S. Everitt. Chance Rules: An Informal Guide to Probability, Risk, and Statistics. Springer-Verlag New York, Inc., New York, NY, USA. 1999.
6. John E. Freund. Modern Elementary Statistics. Pentice-Hall, Inc., Englewood Cliffs, NJ, USA, 1973.
7. J. K. Lindsey. Introductory Statistics: A Modelling Approach. Oxford Science Publications. Oxford University Press, Oxford, UK, 1995.
8. Paul L. Meyer. Probabilidad y aplicaciones estadísticas. Fondo Educativo Interamericano, S. A., México, DF, MEX. 1973. Versión española de la segunda edición de la obra Introductory Probability and Statistical Applications. 1970.
9. Irwin Miller y John E. Freund. Probabilidad y estadística para ingenieros. Tercera Edición. Prentice-Hall Hispanoamericana, S. A., Naucalpan de Juárez, Estado de México. 1985.
10. David S. Moore and George P. McCabe. Introduction to the Practice of Statistics. Fourth Edition. W. H. Freeman and Company, New York, NY, USA. 2003.
11. Emanuel Parzen. Teoría moderna de probabilidades y sus aplicaciones. Editorial Limusa, S.A. de C.V. México, DF, MEX. 1991. Versión autorizada en español de la edición publicada en inglés por John Wiley & Sons, bajo el título de Modern Probability Theory and Its Aplications.
12. Leonard J. Savage. The Foundations of Statistics. Second edition. Dover Publications, Inc., New York, NY, USA. 1972.
13. Taro Yamane. Estadística. Nueva Edición. HARLA S.A. de C.V., México 4, DF, México. 1979.
14. Sharon Bertsch McGrayne. The theory that would not die: How Bayes’ rule cracked the enigma code, hunted down Russian submarines & emerged triumphant from two centuries of controversy. Yale University Press, New Haven, CN, USA. 2011.
15. R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL http://www.Rproject. org/. 2013.