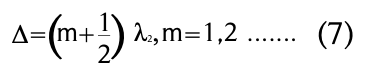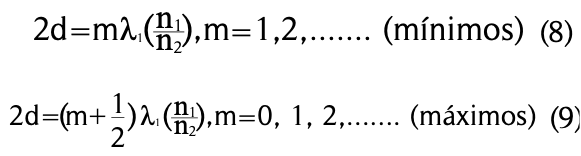Burbujas, la ciencia detrás de su belleza efímera
Enrique Cuauhtémoc Sámano-Tirado* ORCID: 0000-0002-5031-8127
Jorge Miguel Martínez-Rodríguez*, Juan Pablo Rocha-López*
CIENCIA UANL / AÑO 27, No.127, septiembre-octubre 2024
DOI: https://doi.org/10.29105/cienciauanl27.127- 4
RESUMEN
El desarrollo de películas delgadas se debe a su diversidad de aplicaciones en la vida cotidiana. El presente trabajo se centra en burbujas de jabón formadas por películas delgadas. Se realizó un experimento para determinar el grosor mínimo de burbujas a base de agua jabonosa y glicerina mediante la reflexión y refracción de la luz en su superficie. El artículo muestra el modelo matemático que determina el grosor mínimo de la película de jabón. Finalmente, se vincula este experimento con aplicaciones en recubrimientos antirreflejantes en ventanas y lentes. Se resalta cómo un fenómeno cotidiano puede relacionarse con aplicaciones tecnológicas.
Palabras clave: Burbuja, óptica, recubrimientos, glicerina, índice de refracción.
ABSTRACT
The development of thin films is due to their diverse applications in everyday life. This work focuses on soap bubbles formed by thin films. An experiment was conducted to determine the minimum thickness of bubbles based on soapy water and glycerin through the reflection and refraction of light on their surface. The article presents a mathematical model to determine the thickness of the soap film. Finally, this experiment is linked to applications such as antireflective coatings in windows and lenses. It highlights how an everyday phenomenon can be related to technological applications.
Keywords: Bubble, optics, coatings, glycerin, refraction index
Desde la infancia, todos nos hemos maravillado al contemplar el efímero y encantador espectáculo de las burbujas de jabón flotando libremente en el aire. Estos delicados esferoides, llenos de vida y color, nos transportan a un mundo mágico invitándonos a reflexionar sobre los secretos que esconden. Por ejemplo, ¿qué son y cómo se forman las burbujas?, ¿por qué son casi esferas perfectas que se desintegran rápidamente?, ¿por qué tienen esos colores iridiscentes? Las burbujas están conformadas por una película delgada de agua jabonosa que encapsula aire u otro gas.
La pared de éstas consiste en dos láminas, o capas, muy delgadas de jabón con agua en su interior. A continuación analizaremos cómo el equilibrio entre tensión superficial, presión y fuerza de gravedad sobre la película jabonosa determina su sutileza y forma geométrica. Es posible mostrar que, para un volumen dado, la esfera es la figura geométrica que minimiza el área de su superficie que, a su vez, conduce a la disminución de la energía en una burbuja. En física y matemáticas se les conoce como ̈superficies mínimas ̈, una teoría que estudia la manera en cómo se arreglan entre sí las películas de jabón en diversas formas que hagan minimizar su energía (Castelvecchi, 2019).
En una delgada película jabonosa en reposo, las energías que intervienen son la potencial gravitatoria, la de compresión, que ocurre en cualquier volumen de aire atrapado en su interior, y la superficial. En particular, la energía superficial surge como resultado de las fuerzas atractivas entre moléculas a lo largo de la superficie que delimita la película, ésta se expresa en términos de la tensión superficial (Behrouz, 2010).
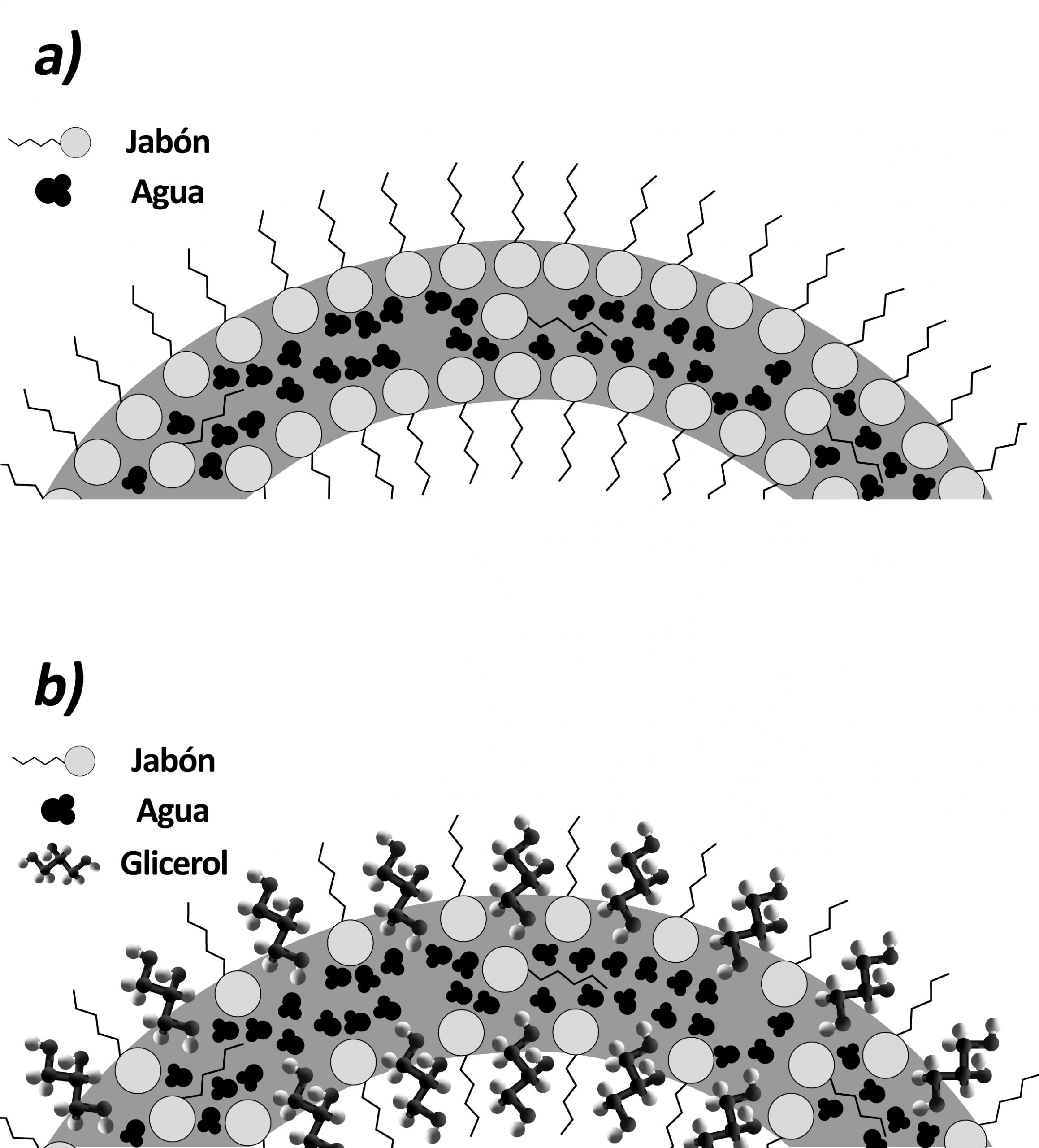
Las moléculas de agua son polares, mientras que las de jabón típicamente consisten en largas pero delgadas cadenas de hidrocarbonos no-polares con un grupo rico en oxígeno altamente polar sólo en uno de sus extremos (Almgren-Junior y Taylor, 1976). Cuando estos dos tipos de moléculas forman parte de una solución homogénea, el extremo no-polar de las de jabón migra hacia las caras interior y exterior de la película jabonosa, pero el segmento polar se orienta para interactuar por medio de puentes de hidrógeno con las moléculas de agua (figura 1a). La superficie de la película así formada se cubre casi por completo con una capa no-polar, resultando en una disminución de la tensión superficial, y teniendo un grosor mínimo aproximadamente igual a la longitud de dos cadenas de moléculas de jabón.
Sin embargo, estas burbujas no son indestructibles, ya que, eventualmente, la misma gravedad se encarga de drenar el líquido contenido en sus superficies, lo que provoca que terminen reventándose. Con la finalidad de determinar el grosor mínimo de las burbujas de jabón y verificar que es del orden de cientos de nanómetros, se llevó a cabo un experimento.
Figura 1. a) Estructura molecular de una burbuja de jabón, y b) al añadir glicerina a la solución.
EXPERIMENTO
Cuando una burbuja es liberada de una varita tradicional, la tensión superficial actúa sobre la delgada película de agua jabonosa que la obliga a adoptar la superficie más pequeña posible y se forma un esferoide. Si la pompa no tuviera aire en su interior, la película de agua con jabón se contraería hasta transformarse en una gota esférica sólida, similar a las gotas de lluvia. Para controlar el tamaño, así como estabilizar y extender la duración de burbujas de jabón, se realizó una mezcla saturada de detergente lavatrastes y glicerina disueltos en agua, y se encontró la proporción adecuada de estas sustancias que incrementa la tensión superficial de las esferas. La durabilidad se debe al aumento de la tensión superficial ya que las moléculas de glicerol se intercalan entre las partículas de jabón en la burbuja (figura 1b), disminuyendo así la evaporación.
Posteriormente, usando una tira de fieltro empapada, se aplica esta mezcla sobre la superficie abierta limitada por el borde de un tazón de vidrio circular, tipo refractario de cocina con un diámetro de alrededor de 25 a 30 cm, al que previamente se le colocó en su interior un trozo de hielo seco sumergido en la misma mezcla. Esto crea una película delgada jabonosa con glicerina que se infla debido al incremento de presión al sublimarse el hielo seco pues el contorno de la película alrededor del borde del tazón funge como sello. Después de unos segundos, la película se hincha hasta formar una gran burbuja hemisférica duradera; es decir, la burbuja no se revienta fácilmente. Por lo tanto, la glicerina en el agua jabonosa hace que se produzcan burbujas de jabón estables, flexibles, casi estáticas con brillantes franjas de color sobre su superficie para el estudio de interferencia de luz en el visible. Una de las burbujas típicas de este experimento se observa en la imagen de la figura 2.
Figura 2. Demostración experimental de la formación de una burbuja de jabón con glicerina.
REFLEXIÓN Y REFRACCIÓN DE LA LUZ EN LA SUPERFICIE DE UNA BURBUJA
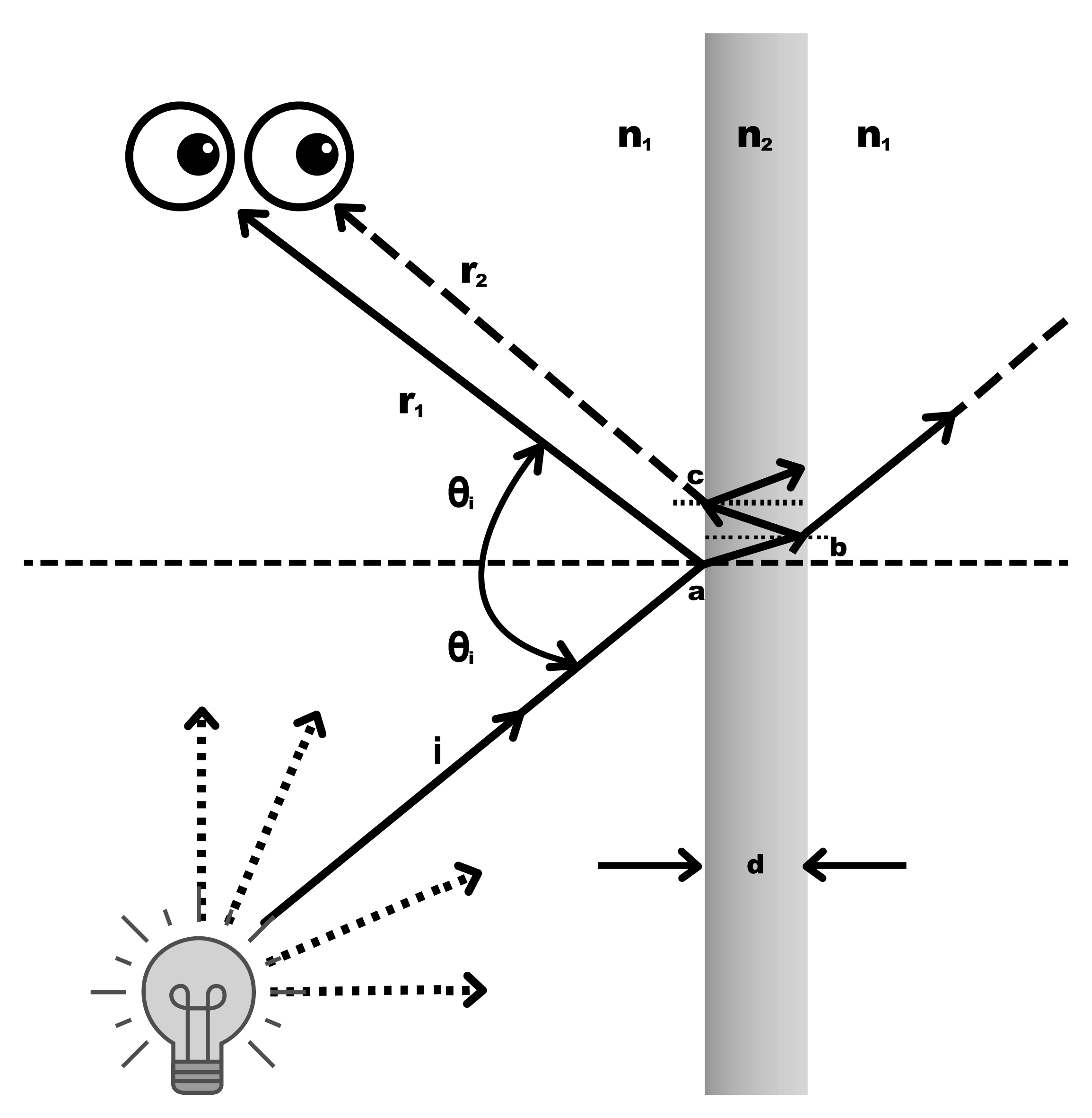
Los brillantes e iridiscentes colores que se observan cuando los rayos de sol, o luz de una lámpara, inciden sobre burbujas de jabón son causados por la interferencia de ondas de luz en el visible provenientes de las caras anterior y posterior de una delgada película de jabón. Esta sencilla observación permite estimar con precisión el grosor de una película de jabón, y cómo aplicar este fenómeno en recubrimientos antirreflejantes.
Figura 3. Reflexión y refracción de la luz en la interfaz de una burbuja.
De acuerdo la figura 3, cuando una onda plana viaja en un medio con índice de refracción n¹ e incide, rayo de luz i, sobre la cara anterior de una delgada película de jabón de grosor d; parte de ese rayo se refleja en a, denotado por r1, con un ángulo θi, idéntico al ángulo del rayo incidente, medido respecto a la normal a la superficie de la película. A su vez, la otra parte del rayo incidente se refracta dentro de la película jabonosa con índice de refracción n² y viaja en su interior. Posteriormente, parte de este rayo refractado se refleja en la cara posterior de la película de jabón en b y otra parte se refracta hacia el medio exterior en que el rayo de luz original incidió en a. Por último, el rayo reflejado en b, viajando dentro de la película jabonosa, se refracta en c, denotado por r², y nuevamente emerge al medio original con índice de refracción n¹. Es posible demostrar que las franjas de colores en las burbujas de jabón se deben a la diferencia del recorrido óptico por los rayos de luz 
, y así determinar bajo qué condiciones la interferencia de estos rayos puede ser constructiva o destructiva. Sin pérdida de generalidad al análisis de este problema, una simplificación razonable es considerar que r¹ incide casi normalmente, θi ≈ 0. Así la diferencia de la trayectoria entre los rayos , denotada por Δ, se obtiene directamente de la figura 3:
Por otro lado, ya que se tiene que la luz viaja por dos medios distintos, la velocidad de los rayos en los medios con índices 
respetivamente, es
Otra forma de escribir las velocidades de los rayos en dos medios distintos es a partir de su definición en términos de frecuencia angular ω y longitud λ para una onda:
La velocidad de la luz es menor a c, 300,000 km/s, cuando un rayo se desplaza en un medio que no sea el aire o el vacío y esto se debe a que la longitud de onda cambia de acuerdo al índice de refracción; pero la frecuencia angular es la misma, 
. De aquí que igualando las ecuaciones (2) y (3), y usando las consideraciones mencionadas, se tiene
En este caso, 
es el índice de refracción en la película de jabón. Entonces, partiendo de (4) se encuentra la relación entre las longitudes de onda λ2, medio jabonoso, con λ1, medio exterior,
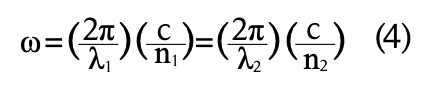
Se muestra en cursos de Física que puede o no ocurrir un cambio de fase de una onda cuando incide sobre una interfaz que separa dos medios distintos, de tal manera que parte se refleja y la otra se refracta (Walker, 2011):
I) Refracción. Nunca hay cambio de fase, sin importar los valores de los índices de los medios que separa la interfaz en los que ocurra.
II) Reflexión. Si la onda viaja en un medio 
hacia la interfaz que separe a un medio , tal que 
no hay cambio de fase. Ahora bien, si la onda viaja en un medio hacia la interfaz que separe a un medio , tal que hay un cambio de fase de 180°; esto es, media longitud de onda (λ/2).
En el presente caso, la diferencia de la trayectoria óptica entre los rayos ocurre sólo cuando la luz viaja en el interior de la película de jabón. Durante este recorrido de la luz, la única interfaz que hace que haya un cambio de fase, λ/2, es cuando la luz se refleja en la cara posterior de la película de jabón en b (figura 3). Por lo tanto, los rayos al reflejarse en a y c, respectivamente, tienen un desfase de λ/2. Considerando lo anterior, se tiene que la interferencia entre los rayos será destructiva (mínimos) cuando la diferencia de la trayectoria Δ sea
y, en consecuencia, la interferencia entre los rayos será constructiva (máximos) cuando Δ sea
Finalmente, sustituyendo (1) y (5) en (6) y (7) se encuentra que
En este caso, la mezcla de agua jabonosa (n = 1.33) con glicerina (n = 1.47), considerando que el volumen de glicerina añadida es 15% del volumen total de la mezcla, resulta en un índice de refracción en la película de = 1.35. Además, la película de grosor d está rodeada de aire; esto es, =1. La foto en la figura 4 muestra una semiburbuja de jabón con glicerina del experimento ya descrito cuando se iluminó con luz solar. Se observa claramente que los colores reflejados en la burbuja son dos franjas alternas: amarilla-verde (A-V), las más intensas, y violeta. Usando la ecuación (9), es posible determinar el grosor d de la película a partir de los colores, por lo que se conocen los valores de λ1, en las franjas de la burbuja y considerando los cantidades de ya dadas. Se tiene que d (m=1)=317 nm y d (m=2) = 370 nm, siendo d ≈ 335 nm el valor promedio, en los colores A-V y violeta, que a su vez se asocian a los máximos de orden m = 1 y 2, respectivamente. Por otro lado, si se sustituye d ≈ 335 nm en (9) tanto para el máximo principal, m=0, como el de orden m=3 se encuentra que λ (m=0) ≈1800 nm yλ (m = 3) ≈ 260 nm, que no se observarían ya que corresponden al infrarrojo (IR) y ultravioleta (UV), respectivamente, fuera del rango visible. Estos resultados se resumen en la tabla I.
El uso de recubrimientos antirreflejantes en ventanas y lentes para disminuir la radiación reflejada en ellos está ampliamente extendida, ya que de esta manera se incrementa la intensidad de radiación transmitida a través de la superficie de un vidrio en el rango visible con este recubrimiento. La reducción de la intensidad reflejada se debe al fenómeno de interferencia de radiación electromagnética, como se mostró ya en las burbujas de jabón con glicerina.
Figura 4. Burbuja de solución jabonosa con glicerina destacando las franjas de colores.
A su vez, la intensidad es una función de la longitud de onda de la luz incidente, el ángulo de incidencia y el índice de refracción de los medios en los que viaja; en particular, el correspondiente a la película delgada que recubre al sustrato, usualmente vidrio. Este diseño es posible al depositar una o varias películas delgadas del material con el índice de refracción adecuado sobre vidrio, siendo aire el medio que rodea al lente o ventana con el recubrimiento antirreflejante (Moss-Mattox, 2004). Por ejemplo, es posible demostrar que la reflectancia es mínima cuando una lente o ventana de vidrio es recubierta con una película delgada de MgF2 si su grosor es aproximadamente igual a un cuarto de la longitud de onda incidente.
CONCLUSIONES
Este trabajo presenta un sencillo y divertido experimento, incluyendo un análisis simple pero preciso, para calcular el grosor mínimo de una película de agua jabonosa con glicerina por medio de la observación del patrón de interferencia constructiva de luz en el rango visible. Este estudio nos hace reflexionar que las burbujas no sólo son estéticamente llamativas, si no que pueden ser útiles al entender aplicaciones tan aparentemente disímbolas como los recubrimientos antirreflejantes.
* Universidad Nacional Autónoma de México, Ciudad de México, México.
Contacto: g10_rocha@ens.cnyn.unam.mx
REFERENCIAS
Almgren-Junior, Frederick Justin, y Taylor, Jean Ellen. (1976). The Geometry of Soap Films and Soap Bubbles, Scientific American, 235(1), 82-93.
Behrouz, Fred. (2010). Surface tension in soap films: revisiting a classic Demonstration, European Journal of Physics, 31, L31-L35.
Castelvecchi, Davide. (2019). US mathematician is first woman to win prestigious Abel Prize, Nature, 567, 295-296.
Moss-Mattox, Donald. (2004). Antireflection (AR) Coatings, Vacuum Technology and Coating, 5(8), 32-33.
Walker, Jearl. (2011). Fundamental of Physics (Halliday & Resnick), Chapter 35, John Wiley and Sons, 973-980.
Recibido: 25/01/2024
Aceptado: 06/05/2024