La Teoría de juegos y la madre naturaleza
José Carlos Pimentel Reyes*
CIENCIA UANL / AÑO 26, No.117, enero-febrero 2023
La teoría de juegos es un cuerpo teórico-matemático que describe las interacciones que establecen dos o más competidores ante una situación de conflicto (juego), e intenta predecir cuál es la mejor estrategia posible para cada jugador teniendo en cuenta las acciones que pueden ejecutar los demás.
Esta teoría parte de la premisa de que todos los contendientes son seres racionales, que eligen las mejores tácticas, afines a sus propios intereses; buscan obtener una recompensa y conocen y siguen las reglas del juego preestablecidas. Los participantes pueden ser personas, instituciones, empresas, gobiernos o individuos de otras especies. La recompensa se entiende como un recurso apreciado y finito (pareja, alimento, territorio). Las estrategias son cualquier acción racional o esfuerzo que llevará a cabo cada adversario para obtener una recompensa. Por otra parte, las reglas del juego son las limitaciones de los jugadores y el contexto en el que se desarrolla la contienda.
Dado lo extrapolable de los elementos de esta teoría, los principios derivados han sido aplicados con éxito en Psicología, Economía, juegos de mesa, el ejército y, por supuesto, en Biología. Quizá uno de los modelos más conocidos, y al que se recurre para ilustrar lo fascinante de esta teoría, es el dilema del prisionero, al que me permito recurrir con una de tantas variaciones que existen:
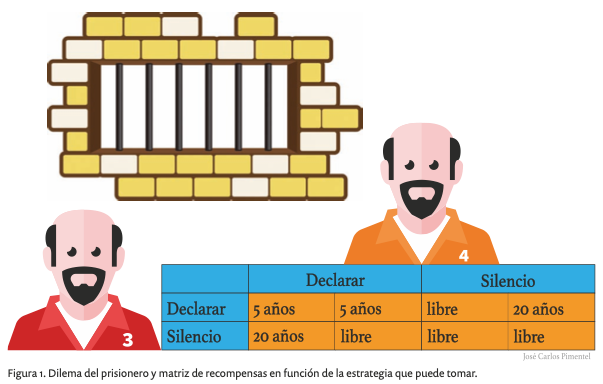
Un fiscal detiene a dos sospechosos de robo a un banco. El fiscal no tiene pruebas suficientes para condenarlos a prisión, por lo que el testimonio de los sospechosos es muy importante para dictar una sentencia. Entonces, el fiscal interroga a los prisioneros en celdas separadas sin que éstos puedan comunicarse entre sí. Le propone a cada sospechoso declarar en contra de su compañero. Si su compañero no declara, el que declare saldrá libre y el otro será condenado a prisión por veinte años. Si ambos declaran mutuamente irán a prisión por cinco años. En cambio, si guardan silencio quedarán libres.
Bajo esta situación, resulta evidente que el plan óptimo para los sospechosos es colaborar guardando silencio, ya que podrán quedar en libertad. Sin embargo, debido a que no tienen posibilidad de comunicarse entre sí, y no tienen certeza que el otro guardará silencio, lo mejor es declarar uno en contra de otro. Así se aseguran de que no obtendrán una pena mayor en caso de que su compañero declare, además, existe la posibilidad de quedar libres en caso de que el otro guarde silencio.
A la actitud de los prisioneros, de culparse mutuamente, en teoría de juegos se le llama equilibrio de Nash. En éste, siguen su mejor estrategia posible, considerando que no pueden comunicarse entre sí y que no hay un pacto que garantice la colaboración.
ESTRATEGIAS EVOLUTIVAMENTE ESTABLES
El equilibrio de Nash ha servido como fuente de inspiración para proponer principios en Biología. Uno de éstos busca entender y predecir situaciones en el juego en las que los planteamientos que adoptan los ejemplares aparentemente ventajosos no se vuelven dominantes entre todos los individuos de una población. Y al mismo tiempo los que aparentemente son desventajosos para la supervivencia de un individuo se mantienen en la población.
Para ilustrar lo anterior, pensemos en el caso de individuos de colibríes que forrajean en busca de néctar floral (recompensa/premio = alimento). Al encontrarse un par de ejemplares cerca de una planta con flores (figura 2), ambos tienen como opciones: a) ser agresivos (pelear por el acceso a las flores) o b) adoptar una actitud pacífica (no pelear).
Si las dos aves eligen a, ambas tienen las mismas probabilidades de obtener una parte del botín; sin embargo, a su vez, la pelea implica un costo en términos de energía y riesgo de salir herido. Por otra parte, si uno adopta a y su competidor b, el primero tendrá acceso a todas las flores de la planta y el segundo nada. En cambio, si escogen b, podrán obtener la mitad del trofeo y evitar los costos de la pelea directa.
Esta situación (adaptación al dilema gavilán-paloma) corresponde a un juego de estrategia mixta en el que se ha establecido una actitud evolutivamente estable (EEE), definida por Maynard-Smith como aquella “…en la que, si todos los individuos de una población la adoptan, ninguna nueva estrategia podría invadir a la población por selección natural”. Bajo estas circunstancias el equilibrio se basa en la permanencia de ambas (agresiva y pacífica) entre los individuos de una población y no puede romperse.
Siguiendo con el dilema del colibrí, sí todos los individuos adoptarán a en cada encuentro, tendrían una menor recompensa en comparación con la elección de adoptar una actitud pacífica, ya que saldrían heridos en cada combate. En este sentido, la aparición de un ejemplar pacífico que prefiere buscar otra fuente de recurso, obtiene la recompensa de no salir herido. Como resultado tendrá mayor éxito reproductivo que los agresivos. Entonces, la táctica pacífica aparecerá en la población, regresando al equilibrio de EEE.
En cambio, si todos los colibríes adoptan b (compartir), la aparición de uno violento sería ventajoso, ya que podría llevarse todo al tiempo que su rival huye. En este escenario, el ofensivo tendría mayor éxito reproductivo que los defensivos. Entonces, la conducta beligerante volvería aparecer en la población, volviendo al equilibrio de EEE.
Bajo este panorama, lo mejor para cada uno de los colibríes es adoptar ambas prácticas, de tal modo que ninguno pueda obtener una ventaja permanente sobre el otro. Determinar cuándo es mejor pelear, huir o compartir para un individuo se abordará más adelante.
DESTRUCCIÓN MUTUA ASEGURADA
Antes de iniciar una disputa por el acceso al alimento, pareja o territorio, los individuos entran en un ritual preconflicto donde se evalúan mutuamente. En este protocolo, también llamado “guerra limitada”, exhiben su musculatura, se ponen lo más erguidos posible, muestran un rostro belicoso y hacen ruidos de intimidación. Si lo anterior no funciona, tienen la opción de empezar la pelea.
El ritual obedece a una maniobra mutua de disuadir al contrario a dar el primer paso, mandando un mensaje de “si te acercas podrás hacerme daño, pero mira con lo que te daré”. Los individuos invierten mucha energía en esto con el fin de evitar llegar a un combate directo, el cual representa un gran costo en términos de energía y un alto riesgo de salir herido. Lo mejor es amenazarse mutuamente con el fin de que ninguno quiera dar el primer paso y después, en el mejor de los casos, cada uno siga su camino.
Lo anterior ha sido descrito en ciencias militares y en Economía como destrucción mutua asegurada (DMA) y en palabras de Thomas C. Schelling obedece a la idea de que “la capacidad de tomar represalias es más útil que la habilidad de resistir un ataque”. Con esta idea los individuos invierten energía en exhibir sus grandes cuernos, colores agresivos, mayor tamaño de garras o colmillos con el fin de disuadir a sus rivales de la pelea.
JUEGOS ASIMÉTRICOS Y SIMÉTRICOS. CUANDO ES MEJOR COMPARTIR, LUCHAR O HUIR
El ritual preconflicto aporta información muy valiosa acerca del estado físico, estatus jerárquico y experiencia del antagonista. Con esta información se pueden valorar las probabilidades que tiene de ganar la pelea, en función de las capacidades que tiene el otro y decidir si se debe o no pelear.
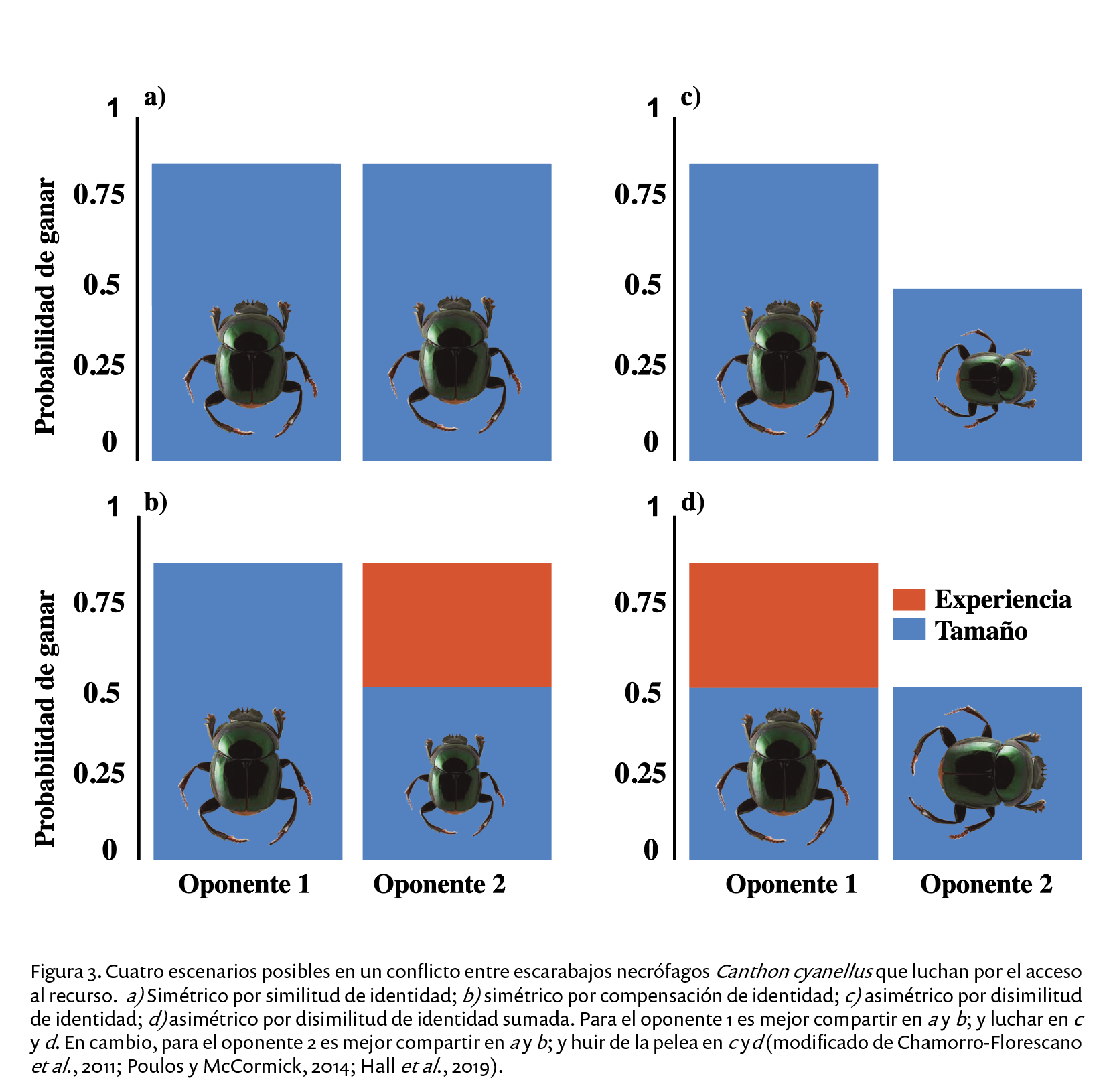
De este modo, si los adversarios tienen las mismas condiciones físicas se habla de un conflicto simétrico por similitud de identidad (figura 3a). En este tipo de enfrentamiento los resultados de las estrategias adoptadas no dependen de la identidad del jugador; ambos tienen las mismas probabilidades de ganar o perder, pero al mismo tiempo salen heridos en la pelea. En estas circunstancias, lo mejor para los dos es compartir.
La actitud pasiva adoptada por los contrincantes ha sido observada en individuos de Canthon cyanellus, una especie de escarabajo necrófago del grupo conocido como peloteros, debido a que construyen una bola de carroña obtenida de algún mamífero muerto en la naturaleza y la ruedan hacia su galería. Esta bola de carroña es fuente de alimento para él y para su descendencia, lo que significa que es muy apreciado. En C. cyanellus ha sido observado que cuando se encuentran individuos que tienen el mismo tamaño (misma probabilidad de ganar/perder) (figura 3a) eligen frecuentemente partir la bola por la mitad. De este modo se aseguran una ración de alimento y evitan el encuentro directo con los costos que implica.
Sin embargo, en otras ocasiones también se ha observado que un individuo de tamaño grande comparte con otro individuo de la misma especie de menor tamaño, cuando este último tiene experiencia exitosa en combate o es acompañado por una hembra (figura 3b). Y viceversa, un individuo pequeño con experiencia o acompañado elige compartir su bola de excremento cuando se enfrenta a un rival de mayor tamaño. En este contexto, estamos en un conflicto simétrico por compensación de identidad (figura 3b), en el que lo mejor sigue siendo ser pacífico y compartir.
Por otra parte, si uno de los sujetos evalúa que tiene una ventaja estratégica sobre el retador (como mayor tamaño) habrá mayores probabilidades de que acceda a entrar en la pelea directa (ser agresivo) ya que tiene mayores probabilidades de ganar. Entonces hablamos de un conflicto asimétrico por disimilitud de identidad (figura 3c), donde los resultados están en función de la identidad del jugador. En esta circunstancia (figura 3c), para el primero resulta ventajoso adoptar una actitud agresiva, y en el caso del segundo una actitud pacífica (huir de la pelea), cediendo el acceso al recurso.
Finalmente, en un cuarto escenario donde los enemigos tienen el mismo tamaño corporal, pero el primero tiene experiencia en combate y el segundo no, estamos en un conflicto asimétrico por disimilitud de identidad sumada (figura 3d). En éste, también observado entre machos de peces damisela (Pomacentrus amboinensis), el primero obtendrá la victoria si escoge agredir, y en el caso del segundo no saldrá lastimado se tiene una actitud pacífica huyendo de la pelea.
¿CUÁNDO UN INDIVIDUO ELIGE COMBATIR AUN CUANDO TENGA MENORES PROBABILIDADES DE GANAR?
Asimismo, existen entornos en los que no es posible colaborar o compartir dada la naturaleza del juego. En éstos el beneficio de uno forzosamente es la pérdida del otro. No es posible la cooperación y no se puede alcanzar un equilibrio.
Podemos observar esto cuando los lobos marinos jóvenes retan al macho alfa a pelear para quedarse con el liderazgo de la manada; no existe la posibilidad de compartir el liderazgo debido a la estructura jerárquica (no se han observado dos machos alfa en una manada). En este caso, ambas partes (macho joven y alfa) se encuentran en las mismas proporciones corporales, pero el macho alfa tiene más experiencia en peleas.
Sin embargo, el alfa tiene un estatus que perder y preferiría no pelear por lo que adopta una técnica disuasiva-agresiva en el ritual preconflicto. No así los jóvenes que no tienen acceso a parejas, por eso elegirán pelear. Otro ejemplo es el de los insectos que tienen periodos de vida adulta muy cortos (algunos sólo un día), por lo que se ven presionados a competir por el acceso a una pareja aun cuando estén en un juego asimétrico (menor tamaño, menor simetría corporal, colores menos llamativos en comparación con sus congéneres). En este caso, el riesgo de no competir es mayor que pelear, ya que si eligen no competir no tendrán ninguna oportunidad de dejar descendencia.
LA TEORÍA EN NUESTRAS RELACIONES INTERPERSONALES
Los principios derivados de la teoría de juegos, y observados en el reino animal, son perfectamente extrapolables y consistentes con las relaciones que establecemos las personas a nivel familia, comunidad y gobierno. De esta teoría podemos entender situaciones cotidianas que, vistas desde una perspectiva ética, son injustas, pero cumplen con los principios de la teoría. Imaginemos un dictador de un país equis tendrá relaciones de coexistencia con sus países vecinos (misma capacidad de perder/ganar + daño ocasionado por la pelea) ya que se encuentra en un conflicto simétrico por similitud de identidad (figura 3a). Sin embargo, este mismo dictador no tendrá reparo en practicar violencia contra sus ciudadanos, ya que se encuentra en un conflicto asimétrico por disimilitud de identidad (mayores posibilidades del dictador de ganar; figura 3c).
De estas situaciones, que también son observadas en las relaciones intraespecíficas de las especies (los individuos de C. cyanellus por mencionar alguno), podemos aprender las lecciones y usar nuestro ingenio para romper las asimetrías que no favorecen la colaboración. Pudiera ser compensando las deficiencias con un aumento en experiencia, poder de colectividad, capacidad de represalia. Es importante recalcar que para que sea posible la colaboración, además de tratarse de una contienda simétrica, debe darse en un entorno donde los contendientes puedan valorarse mutuamente para saber que están en las mismas condiciones de ganar. Más allá, donde puedan confiar en el beneficio mutuo para que funcione, si no, caeríamos nuevamente en el dilema del prisionero donde los sospechosos se atacan mutuamente debido a que no tienen posibilidad de comunicarse y pactar.
Una forma en la que las personas confían en que el opositor colaborará es estableciendo normas y penas para el que las incumpla. Ahora imaginemos una comunidad en donde los ciudadanos participan del cuidado y los beneficios de un huerto. En este caso, los ciudadanos egoístas (que no colaboran en el mantenimiento, pero sí gozan de los beneficios) se encontrarían en una situación de ventaja ya que se ahorrarían el esfuerzo de cuidar el huerto. Al mismo tiempo, esto haría que más personas quisieran adoptar la misma práctica egoísta llegando a un juego de estrategias mixtas, donde habrá unas personas que participarán en el cuidado del huerto y otras no.
Sin embargo, la penalización a la persona egoísta ayudará a disuadir a los demás de ser iguales. La colaboración siempre será la mejor opción donde todos salen beneficiados. En cambio, una actitud individualista no favorece lo óptimo posible (ver dilema del prisionero).
Finalmente, una muestra de una actitud individualista se ha observado recientemente en la distribución mundial de las vacunas ANTICOVID-19. Los países con mayores ingresos acapararon gran parte de las vacunas producidas con el fin de inmunizar a sus ciudadanos. Lo anterior ocasiona que los países de bajos ingresos no logren acceder en tiempo y forma a una parte significativa de éstas.
Tal distribución desigual ha estado ocasionando que aparezcan nuevas variantes del coronavirus entre los países rezagados (ómicron en África), que vuelven a poner en peligro los logros alcanzados a nivel mundial. Aunque esta actitud individualista entre los países más poderosos cumplió con el equilibrio de Nash, es evidente que una distribución equitativa de las vacunas hubiera sido la mejor opción. Como dijo Bill Gates “(…) ayudar no sólo es lo correcto, sino que es lo más inteligente”. Lo mejor siempre será colaborar, tomar sólo lo que necesites, esperar tu turno y confiar en el poder colectivo, es lo que nos muestra la naturaleza y las matemáticas…
AGRADECIMIENTOS
El autor agradece a Fernando Gervacio, al Bio. Martín de los Santos, a la Dra. Isabelle Barois, al Dr. Mario Favila y a dos revisores anónimos por sus observaciones y comentarios a borradores previos.
*Instituto de Ecología, A.C., Xalapa, Veracruz.
Contacto: charly-eco.ip@hotmail.com
REFERENCIAS
Chamorro-Florescano, I.A., Favila, M.E., y Macías-Ordóñez, R. (2011). Ownership, size and reproductive status affect the outcome of food ball contests in a dung roller beetle: when do enemies share? Evolution Ecological. 25:277-289.
Dawkins, R. (1993). El gen egoísta, las bases biológicas de nuestra conducta. Oxford University Press.
Hall, C.L., Porter, M.A., y Dawkins, M.S. (2019). Dominance, Sharing, and Assessment in an Iterated Hawk-Dove Game. Journal of Theoretical Biology. 110101.
Poulos, D.E., y McCormick, M.I. (2014). Who wins in the battle for space? The importance of priority, behavioural history and size. Animal Behaviour. 90:305-314.
Sánchez, A. (2006). Las matemáticas de la cooperación humana. Matematicalia. 2(3). Disponible en: http://www.matematicalia.net/index.php?option=- com_content&task=view&id=252&Itemid=169.
Stokel-Walker, C. (2015). ¿Qué es exactamente la teoría de juegos? BBC. Disponible en: https://www.bbc.com/mundo/ noticias/2015/02/150220_teoria_de_juegos_que_es_finde_dv.
Zapardiel-Quirós, C. (2014) La teoría de los juegos y sus aplicaciones en la economía actual. [Tesis de Licenciatura] Universidad Pontificia Comillas, Madrid. Disponible en: https://repositorio.comillas.edu/rest/bitstreams/1184/retrieve