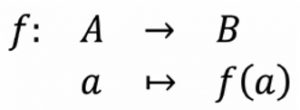UN INFINITO MÁS GRANDE

donde, en lugar de escribir 𝑓(𝑎), se suele escribir la descripción general de la asignación de cada elemento 𝑎

¹ En realidad, no toda propiedad “formal” puede definir un conjunto. Por ejemplo, si existiese un conjunto de la forma 𝐴 = {𝑥/𝑥∉𝑥} llegaríamos a una contradicción (¿se cumple 𝐴∈𝐴?); a esto se le conoce como la paradoja de Rusell.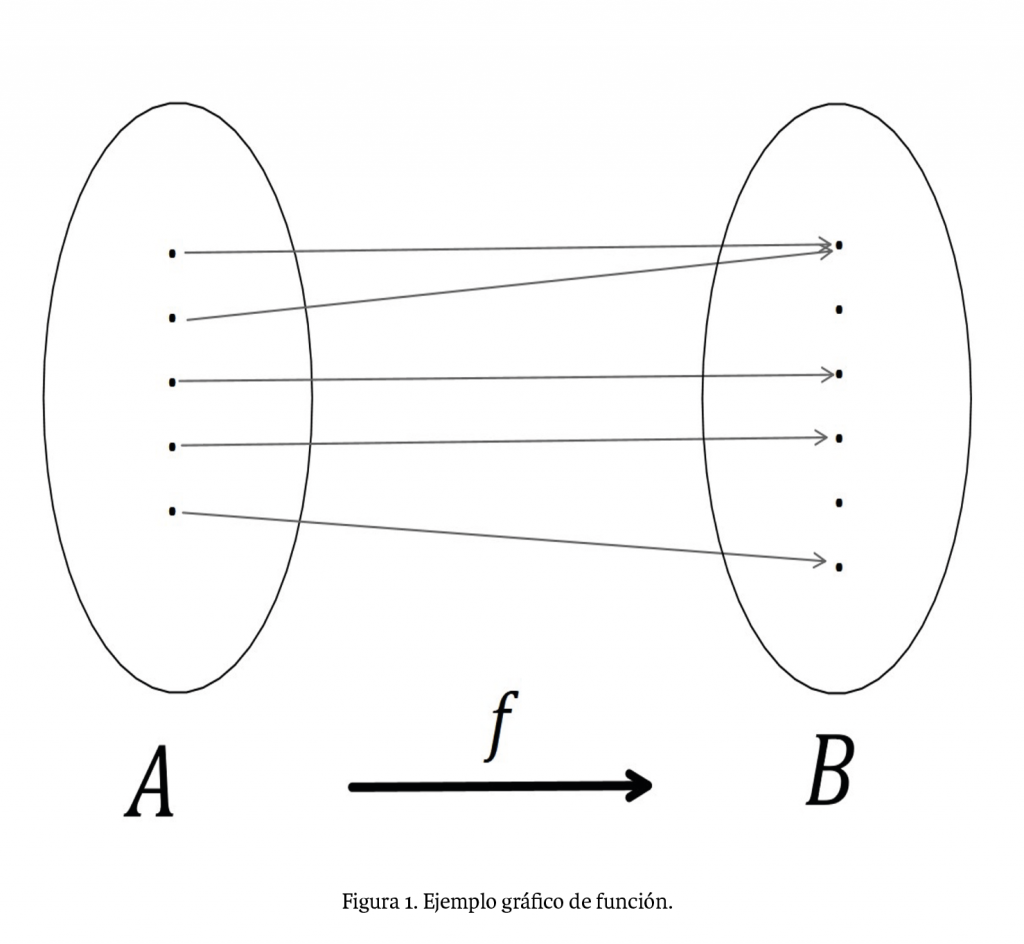

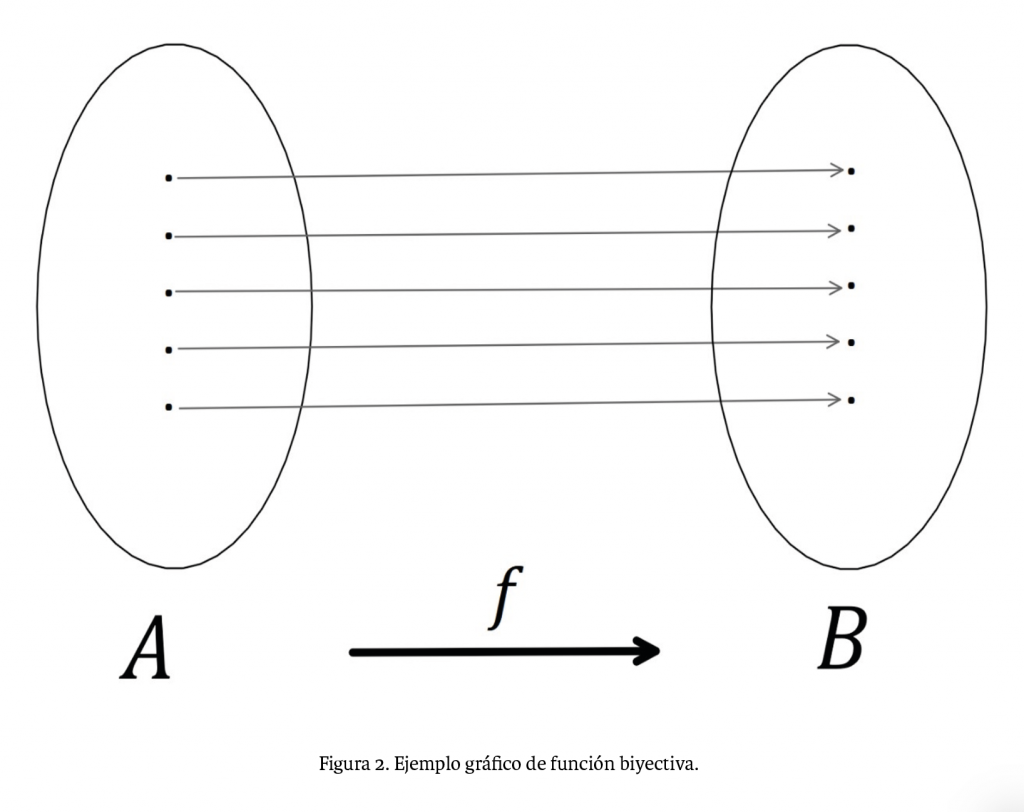
Decimos que una función 𝑓:𝐴→𝐵 es biyectiva si a cada elemento del segundo conjunto le corresponde un único elemento del primer conjunto (véase figura 2).

CONJUNTOS FINITOS E INFINITOS

Decimos que dos conjuntos 𝐴 y 𝐵 tienen el mismo tamaño si existe una función 𝑓:𝐴→𝐵 biyectiva, y si 𝐴 tiene el mismo tamaño que un conjunto 𝐴 ={0,1,…,𝑛 – 1}, decimos que es 𝐴 finito y tiene 𝑛 elementos. Un conjunto es infinito si no es finito.

Por ejemplo, ℕ es infinito. Sin importar cómo le asignes elementos de 𝐴 a ℕ, siempre van a faltar números por cubrir.

Cuando dos conjuntos 𝐴 y 𝐵  tienen el mismo tamaño, se suele decir que tienen la misma cardinalidad y se escribe |𝐴|=|𝐵|, donde |𝐴| denota el “número de elementos” que tiene el conjunto 𝐴, aunque su número de elementos sea “infinito”.

Ejemplos conocidos de conjuntos infinitos son los de números pares, primos, enteros, racionales y reales.

El conjunto de los números enteros consta de los números naturales y todos sus negativos; lo denotamos como ℤ={…,–2,–1,0,1,2,….}. El conjunto de números racionales es el conjunto de aquellos números conocidos comúnmente como fracciones; lo denotamos como

Números enteros como –2 se pueden expresar como números racionales mediante  –2/1, por lo que todo número entero es racional.

El conjunto de números reales (denotado como ℝ) es un poco más difícil de definir. Nos sirve pensar en un número real como un arreglo infinito de números, donde el primer número es un número entero y el resto (los decimales) son números naturales entre el 0 y el 9. Números racionales como 1/3 se pueden expresar dentro del conjunto de números reales como 0.33333…, por lo que abreviamos simplemente escribiendo 1/3. Un ejemplo famoso de número real que no es racional (en cuyo caso solemos llamarles números irracionales) es π=3.1415926535…

Otra forma de describir un número real es mediante una suma , donde los números a son elementos de {0,1,…,9}, a excepción del primero (𝑎₀), que puede ser cualquier número entero. Por ejemplo, –20.12333… se puede escribir como:

Los conjuntos ℤ,ℚ y ℝ son ejemplos de conjuntos infinitos. Cabe preguntarse, ¿son del mismo tamaño? La intuición nos puede decir dos cosas: por un lado, tenemos que ℕ⊊ℤ⊊ℚ⊊ℝ, por lo que parece razonable pensar que son conjuntos consecutivamente más grandes que el otro. Otra intuición nos dice que todos son infinitos y por lo tanto tienen el mismo tamaño, su tamaño es el  “infinito”. Sin embargo, como veremos en las siguientes secciones, ambas suposiciones son erróneas.

CONJUNTOS NUMERABLES

Un conjunto es numerable si existe una función biyectiva entre éste y ℕ. La idea intuitiva de que un conjunto X sea numerable es pensar que sus elementos se pueden enlistar u ordenar, seleccionando un primer elemento, luego un segundo, un tercero y así sucesivamente. A pesar de que ℤ y ℚ son conjuntos que contienen a los naturales, resulta que son numerables, tienen el mismo tamaño que ℕ.

Para enlistar a los números enteros podemos escoger como primer elemento al cero, luego etiquetar a todos los naturales, cada uno seguido de su negativo (la lista resultante sería 0,1,1,2,2,3,3,…) y, como podemos imaginar, se terminará enlistando a todos los enteros.

Puede sonar algo raro que los racionales sean numerables, ya que desde luego hay una cantidad infinita de racionales, pero, a diferencia de los números naturales y enteros, entre cualesquiera dos racionales hay una infinidad de ellos. Para exhibir la numerabilidad de los racionales probaremos que el conjunto de racionales no negativos (denotamos a este conjunto como ℚ⁺) es numerable, ya que si ℚ⁺ es numerable, se pueden ordenar los racionales negativos usando el mismo argumento que utilizamos con los enteros (el proceso de alternación de signos). Empezaremos escribiendo todos los naturales, luego, debajo de éstos escribiremos los naturales divididos entre dos, luego escribimos los naturales divididos entre tres y así sucesivamente. Luego tomaremos la numeración en diagonal, cada diagonal se tomará de izquierda a derecha, de tal forma que se termina con cada uno de los elementos de ℚ⁺ (véase figura 3). Hay que resaltar que en el orden que dimos para los racionales hay números que aparecen más de una vez (por ejemplo, 0/1=0/2), pero podemos simplemente saltarlos. De lo anterior podemos concluir que ℚ⁺ es numerable. De modo que, como ya mencionamos, haciendo uso de la alternación de signos, se puede construir una numeración de todos los racionales.

Así, a pesar de que ℕ⊊ℤℚ⊊Q, los tres conjuntos son numerables, es decir, tienen la misma cardinalidad. ¿Será que todos los conjuntos infinitos tienen el mismo tamaño?

INFINITOS MÁS GRANDES QUE OTROS

Después de saber que |ℕ|=|ℤ|=|ℚ|, resulta sorpresivo descubrir que ℝ es más grande que ℕ. Mostraremos que existe A⊂ℝ no numerable, y dado que hay una parte del conjunto de los reales que no es numerable, en general ℝ es no numerable. Consideraremos al conjunto (0,1), el cual consta de todos los números reales entre cero y uno.

Si suponemos que (0,1) es numerable, entonces podríamos enlistarlo, como lo muestra la figura 4 (la cual exhibe los primeros cinco números), donde el 𝑘-ésimo número real tiene expansión en decimales como se ve en la imagen. Ahora, por el supuesto, todos los números reales deben estar en la lista. Denotamos al 𝑖-ésimo decimal del 𝑖-ésimo número real como 𝑑ᵢ,ᵢ. Consideremos a un número real entre cero y uno, donde elegiremos, para cada decimal 𝑖-ésimo Dᵢ, cualquier número distinto de 𝑑ᵢ,ᵢ. El número real 𝑥 debería estar en la lista de los números reales, de modo que 𝑥=𝑛_k para algún 𝑘∈ℕ, o bien, 𝑥 sería el 𝑘-ésimo número real, donde su 𝑘-ésimo decimal es 𝑑_k,_k, pero el 𝑘-ésimo decimal de 𝑥 es D_k, donde D_k≠𝑑_kk, de modo que 𝑛_k≠𝑥, lo cual es una contradicción. Por lo tanto, podemos concluir que el conjunto (0,1) no es numerable, de modo que ℝ no es numerable.

La anterior prueba, que consistió en construir un número tomando decimales distintos a los de la diagonal de una hipotética lista de números reales, es comúnmente llamada diagonal de Cantor. La demostración de la no numerabilidad de ℝ fue formulada por primera vez por Georg Cantor en 1874, pero sería después cuando añadiría el argumento de la diagonal (véase Ferreirós (2008) para éste y otros detalles históricos de la teoría de conjuntos).

CONCLUSIÓN

Resulta que hay conjuntos infinitos de distintos tamaños. Expusimos aquí dos de estos “infinitos”, el infinito de ℕ y el de ℝ, pero hay incluso más, infinitos más (el lector puede investigar más en Gracián (2014), o aventurarse a un estudio formal de Hernández (1998) o Hrbacek y Jech (1999)).

La diferencia entre tamaños de dos conjuntos infinitos no está determinada por el que uno esté contenido en el otro, pues como pudimos ver |ℕ|=|ℤ|=|ℚ|.

Estos resultados pueden parecer contraintuitivos o paradójicos, pero en realidad son consecuencias de la definición precisa de conjunto infinito, una definición que nos demuestra el poder de las Matemáticas para dar luz a las ideas más desafiantes. El infinito no es inalcanzable para la razón humana, es un objeto matemático.

 

REFERENCIAS

Hernández, F.H. (1998). Teoría de conjuntos. México: Sociedad Matemática Mexicana.

Fresán, J. (2010). El sueño de la razón: la lógica matemática y sus paradojas. México: RBA Coleccionables.

Gracián, E. (2014). Un descubrimiento sin fin: el infinito matemático. México: RBA Coleccionables.

Hrbacek, K., y Jech, T. (1999). Introduction to set theory, revised and expanded. Nueva York: Crc Press.

Ferreirós, J. (2008). Labyrinth of thought: A history of set theory and its role in modern mathematics. Springer Science y Business Media.

Jech, T. (2013). Set Theory: The Third Millennium Edition, revised and expanded (Springer Monographs in Mathematics). Springer.

Halmos, P. R. (2017). Naive set theory. Nueva York: Courier Dover Publications.