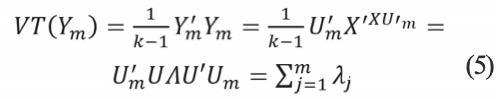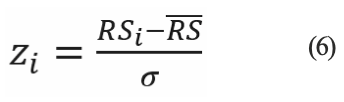Análisis del componente principal para reducir datos de radiación solar, caso de estudio Monterrey, Nuevo León

Los modelos de optimización empleados para definir el dimensionamiento o los criterios de operación de un SE son susceptibles a la calidad de datos de entrada suministrados. Un modelo que haya sido validado con datos poco confiables no representará correctamente la realidad. Mientras que un modelo que haya sido validado con bases de datos reales muy densas provocará elevados costos computacionales. Por esto, existe esa búsqueda por encontrar el equilibrio en el que una base de datos sea suficientemente representativa para lograr un correcto desempeño del modelo y simultáneamente sea suficientemente pequeña para que no signifique un alto costo computacional. Por estas características, es un objetivo común en trabajos de investigación reducir el número de datos que se ingresan en modelos matemáticos o numéricos de optimización de los SE, buscando mantener suficiente información de los datos de entrada, de manera que sean representativos de la muestra real (Kettaneh, Berglund y Wold, 2005). Esto beneficia al operador de estos modelos, ya que simplifica y aligera el proceso de cálculo relacionado con los SE, conforme se reduce la información de entrada, favoreciendo un procesamiento más eficiente y con menor costo computacional (Rı, 2012). 

En el caso que se revisa en este trabajo, se utiliza un algoritmo que permite la reducción de la información de una base de datos de radiación solar: el análisis de componente principal (ACP). Las mediciones corresponden a una estación meteorológica ubicada en Monterrey, Nuevo León. Las variables que se registran en la estación meteorológica son Temperatura ambiente, Radiación solar global, Velocidad de viento, entre otras. Las características del equipo que mide la radiación solar global empleada en este estudio pueden encontrarse en la ficha técnica del producto (Fluke Corporation, 2020). Para lograr la reducción deseada se aplicaron algunos criterios heurísticamente, logrando disminuir significativamente la densidad de los datos de entrada conservando mucha de la variabilidad de los datos originales. 

GENERALIDADES DEL ANÁLISIS DE COMPONENTE PRINCIPAL (ACP)

El análisis de componente principal (PCA, por su acrónimo en inglés, Principal Component Analysis), aquí ACP, es una técnica estadística que permite identificar aquellos valores que representan mejor las características de una cierta base de datos analizada, debido a que se descomponen medidas reales en m componentes principales (CP), los cuales representan diferentes porcentajes de la varianza de los datos analizados (Wang y Xiao, 2004).

Inicialmente se tiene una matriz X con k filas o mediciones y n columnas o dimensiones. El objetivo de aplicar ACP a un conjunto de datos de n dimensiones es hacer una reducción del número de datos necesarios para modelar el comportamiento de una determinada variable utilizando menos dimensiones, pero manteniendo cierta representatividad de los datos originales (Islas Arizpe et al., 2007).

En ACP se busca una correlación lineal de las columnas de la matriz X con la máxima varianza, esta combinación lineal está dada por , donde a es un vector de constantes a uno con a₁ ,a₂ ,…,a_p. La varianza de dicha combinación lineal está dada por var(Xa) = a‘Sa, donde S es la matriz de covarianzas (Jollife y Cadima, 2016).

Posteriormente se calcula la matriz de covarianzas (S): encontrando aquellos eigenvectores de la muestra que tengan los m eigenvalores mayores para colocarlos como las columnas de dicha matriz que se forma realizando las operaciones con la matriz de carga U (S= U⋀U^T) también puede expresarse como:

donde X es la matriz en la que aparecen las n muestras de las variables originales (cada fila). Las columnas de esta matriz son los eigenvectores de S, de forma que U se define como:

Finalmente, los componentes principales y (Y ∈ 𝕽ⁿ) son entonces construidos mediante la operación:

Para lograr la reducción de dimensionalidad de la muestra analizada deben seleccionarse los m primeros eigenvectores de ambas matrices, que tendrán la mayor variabilidad. 

Así, la suma de los m autovectores conservados indicará la variabilidad de la matriz :

Para mayores detalles de éstas y otras deducciones de PCA refiérase a Jollife y Cadima (2016) y Grané y Jach (2014).

En general, PCA reduce la dimensionalidad de una muestra estadística al reconocer las variaciones más relevantes de la muestra analizada. De forma que pueden resolverse modelos de cálculo con suficiente cercanía al comportamiento de los datos a pesar de utilizarse menos entradas.  

METODOLOGÍA Y CASO DE ESTUDIO

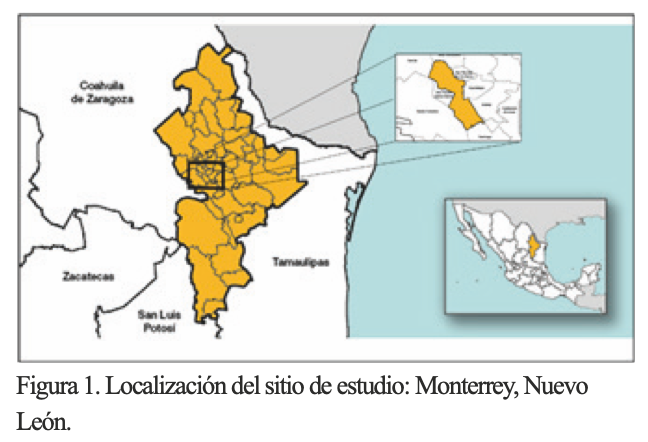
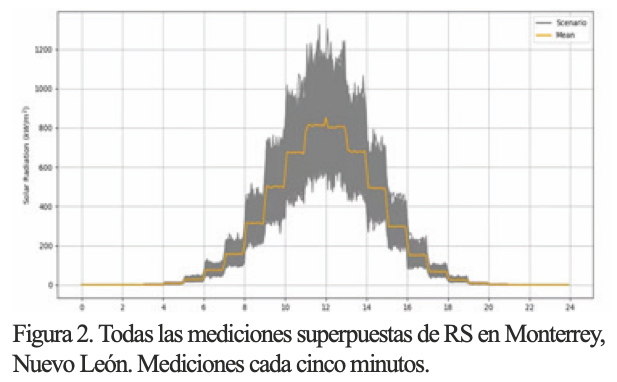
En la figura 1 se muestra la ubicación de Monterrey, Nuevo León, sitio de nuestro caso de estudio. Mientras que en la figura 2 aparecen todas las mediciones de RS en el sitio estudiado, se usa un gráfico de superposición de los datos para resaltar que hay fluctuaciones importantes a lo largo del año que se observan en el gráfico. También se presenta el día promedio del año que, evidentemente, no logra captar el comportamiento de esta variable. 

Primero se eliminan algunos valores atípicos que pueden modificar las características de la muestra estadística (outliers) mediante truncamiento (Wilks, 1963): simplemente, aquellos valores que exceden el valor máximo admisible de radiación solar son eliminados y sustituidos por el promedio de los datos de los días circundantes para esa hora del día. Como valor máximo de radiación se decidió utilizar 1300 W/m². Los datos atípicos pueden deberse a errores de los equipos, mal funcionamiento o mala interpretación de información o de observaciones reales esporádicas (Kettaneh, Berglund y Wold, 2005).

En el caso de estudio se usó un normalizador estándar (Jollife y Cadima, 2016) cuya fórmula para obtener cada término de la serie es:

donde RS_i es la observación, RS es la media del conjunto y σ es la desviación estándar de esa muestra.

En este caso de estudio se analiza una serie de tiempo de un año completo de mediciones de irradiación solar. Los datos tienen una frecuencia cada cinco minutos. Los datos totales analizados son 105,120 datos. Tras el preprocesamiento mínimo, se decidió dividir la serie en cuatro periodos, debido a que se desea incluir el comportamiento de cada estación climática del año. El inicio y fin de cada periodo se seleccionó con base en las siguientes condiciones: los cuatro periodos deben contener la misma cantidad de datos n, los cuales deberán cubrir un periodo correspondiente a una estación climática. El periodo 1 (P1) va del día 1 al 96, el periodo 2 (P2) del 97 al 192, el periodo 3 (P3) del 174 al 269 y el periodo 4 (P4) del día 270 al 365. Como se observa, hay un traslape de 18 días entre los periodos 2 y 3, sin embargo, esto no representa demasiados cambios en las características principales de cada periodo, ni variaciones significativas en el ACP. 

Para encontrar un CP de cada periodo se decidió utilizar una distribución tal que se lograra la mayor reducción mediante la siguiente secuencia: inicialmente, se tienen 96 días de observaciones (27,648 datos), se dividen en dos series, para ser consideradas como dos dimensiones, cada una de éstas con 48 días (13,824 observaciones). Tras este paso se normaliza la información y se aplica el ACP, obteniendo dos CP cada uno con 13,824 datos, donde el componente principal 1 (CP1) tiene una representatividad alta (superior a 97% de los datos originales), mientras que CP2 es desestimado. Después, el CP1 de esta iteración es tomado como una nueva serie, por lo que se divide en dos partes, cada una de 24 días, y se repite el proceso del ACP para la información remanente. Esto se repite cuatro veces hasta reducir los datos a tres días representativos. Finalmente, los tres días representativos deben escalarse al rango real. En la figura 3 se observa un diagrama de flujo con este procedimiento.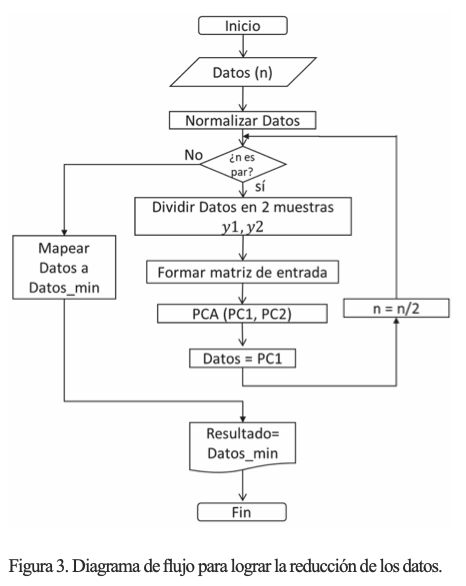

RESULTADOS Y DISCUSIÓN

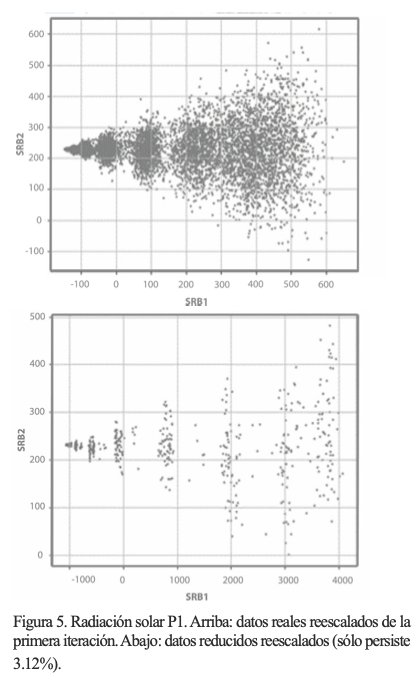
Los resultados del ACP para el P1 se muestran en la figura 4, en donde se aprecia cómo el comportamiento de los datos después de cada iteración sigue similar, ya que siguen una tendencia de 45° aproximadamente. Surgen varios grupos de datos a lo largo de esa recta, siendo cada vez más dispersos a valores mayores de los CP respectivos, note que la escala en cada iteración se altera un poco, pero no demasiado. En este caso se observa este comportamiento debido a que, aún analizados sin tratamiento previo, los datos solares tienden al comportamiento Gaussiano. Observe cómo, en la figura 5, los CP de la primera y última iteración son reescalados para formar los días representativos de P1. El proceso de reescalamiento obedece a un mapeo para trasladar los resultados normalizados al rango original.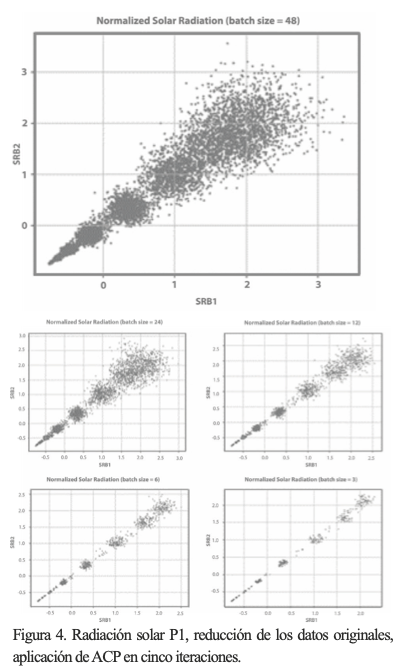

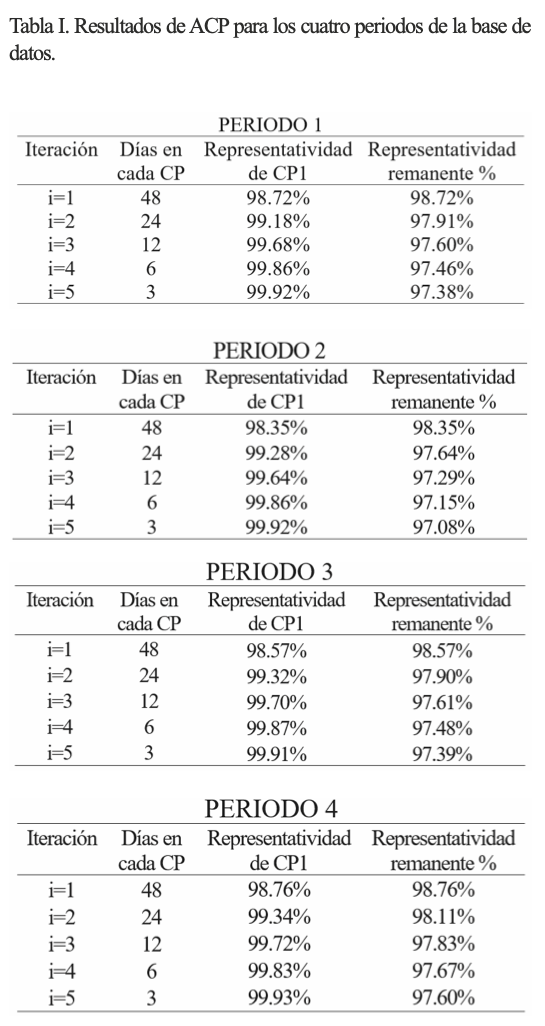
Para poder analizar cuantitativamente los resultados, se debe identificar la proporción del eigenvector del CP analizado, siendo un valor entre 0 y 1, el porcentaje de representatividad se obtiene al multiplicarlo por 100%. Estos resultados se observan para los cuatro periodos en la tabla I. Dado que en cada iteración se pierde información, se registra la representatividad del CP1 para cada una de ellas en porcentaje, y se multiplican entre sí, esto es, si se alcanza 90% en la iteración 1 y 95% en la iteración 2, representa realmente 85.5% remanente del total, y así sucesivamente.

En la tabla I se presentan los resultados de cada periodo, observe que los tres días resultantes de cada periodo representan un porcentaje alto de la información pertinente en ese periodo. Se debe recordar que de 27,648 datos se reduce a 864 por periodo, por lo que valores de representatividad por encima de 90% se consideran altos.

En la primera iteración en cada periodo se agrupa la varianza de todo el conjunto con valores superiores a 98%, debido a que el primer paso en esta metodología es el que produce mayor pérdida porcentual de los datos sometidos a ACP, esto indica que en los pasos posteriores la reducción porcentual no será tan elevada. Finalmente, se reduce la información con ACP hasta sólo quedar 3% del número de datos originales, sin embargo, aún permanecen valores superiores a 97% de la varianza de los datos originales, por lo que, estadísticamente, son representativos de la muestra analizada.

En la figura 6 se observan los días representativos para los cuatro periodos, respectivamente. Note que para cada hora del día hay 12 valores (por ser medidas cada cinco minutos) y que éstas aparentan describir una curva tipo campana cada 24 horas, aunque con una especie de escalones, ya que existe una cierta concentración alrededor del promedio en cada hora del día, quizá debido a que se trata de un subconjunto de datos. Esto no es atípico, sobre todo si se considera que estos resultados provienen de temporadas estacionales de un año calendario.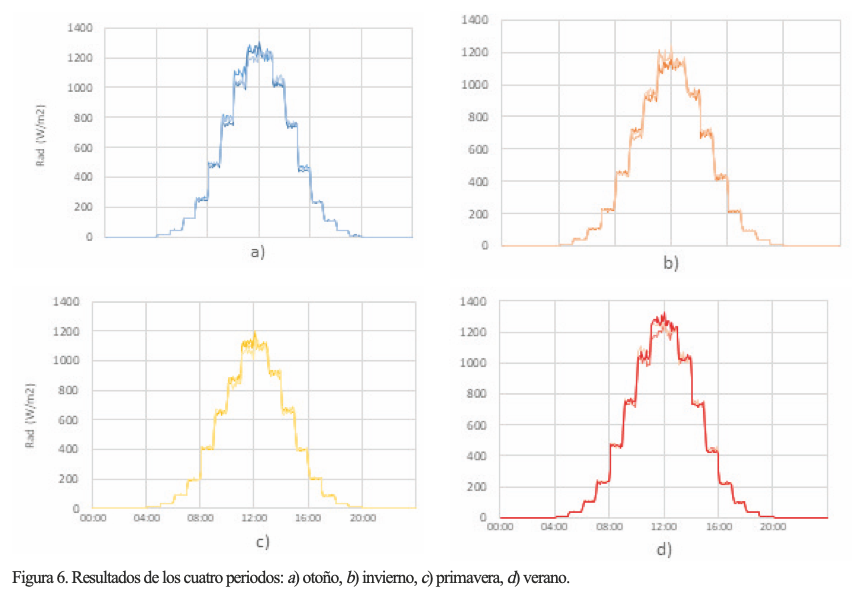

CONCLUSIONES

En este trabajo se incluye el análisis de una muestra de radiación solar de Monterrey, Nuevo León, a la que se le realizó un ACP con la intención de reducir su dimensionalidad. Se dividió el conjunto en cuatro subconjuntos que coinciden con el inicio de las estaciones del año, aproximadamente, para obtener series representativas de cada estación. Se observa que los resultados fueron similares para cada periodo, y que son el CP final; la RS alcanza valores por encima de 97% de representatividad, mientras que reduce la cantidad de datos hasta aproximadamente 3%. La precisión del análisis se debe a que la RS, por su naturaleza, tiene un comportamiento Gaussiano. El ACP, por su formulación, es más preciso para este tipo de variables. Es posible reducir más los datos para obtener sólo un día representativo de cada periodo, lo cual se analizará en un trabajo a futuro. También se plantea el análisis de otras variables involucradas en el modelado de SE como la velocidad del viento o la demanda energética. 

 

* Instituto Nacional de Enfermedades Respiratorias “Ismael Cosío Villegas”,
Ciudad de México, México.
Contacto: marielmb@comunidad.unam.mx

REFERENCIAS

Cadenas, E. et al. (2019). Wind speed variability study based on the Hurst coefficient and fractal dimensional analysis. Energy Science & Engineering. 7(2):361-378. Doi: 10.1002/ese3.277
Cadenas, E., y Rivera, W. (2010). Wind speed forecasting in three different regions of Mexico , using a hybrid ARIMA e ANN model. Renewable Energy. Elsevier Ltd. 35(12):2732-2738. Doi: 10.1016/j.renene.2010.04.022
Islas Arizpe, J.L. et al. (2007). Aplicación de análisis de componente principal en sistemas eléctricos de potencia. Ingenierias UANL.  X(34):51-58.
Fluke Corporation. (2020). Medidor de radiación solar Fluke IRR1-SOL. Medidor de radiación solar Fluke IRR1-SOL. Madrid, Madrid, España. Disponible en: https://www.redeweb.com/ficheros/catalogo-medidor-irradiancia-solar.pdf
Grané, A., y Jach, A. (2014). Applications of principal component analysis (PCA) in food science and technology. In Daniel Granato y Gastón Ares (edit.). Mathematical and statistical methods in food science and technology, pp. 57-87.
Jollife, I., y Cadima, J. (2016). Principal component analysis: a review and recent developments. Philosophical Transitions A. Royal society. 374(2065):1-16. Doi:http://dx.doi.org/10.1098/rsta.2015.0202
Kettaneh, N., Berglund, A., y Wold, S. (2005). PCA and PLS with very large data sets. Computational Statistics and Data Analysis. 48:69-85. Doi: 10.1016/j.csda.2003.11.027
Martínez-Álvarez, F. et al. (2015). A Survey on Data Mining Techniques Applied to Electricity-Related Time Series Forecasting. Energies. 8(11): 13162-13193. Doi: 10.3390/en81112361
Rangel, E., et al. (2020). Enhanced Prediction of Solar Radiation Using NARX Models with Corrected Input Vectors. Energies. 13(10):1-22. Doi: 10.3390/en13102576
Luna-Rubio, R, et al. (2012). Optimal sizing of renewable hybrids energy systems : A review of methodologies. Solar Energy.  86(4):1077–1088. Doi: 10.1016/j.solener.2011.10.016
Tiwari, G.N., Tiwari, A., y Shyam. (2016). Handbook of Solar Energy. Springer Science+Business Media Singapore. Doi: 10.1007/978-981-10-0807-8
Wang, S. y Xiao, F. (2004). AHU sensor fault diagnosis using principal component analysis method. Energy and Buildings. 36(2):147-160. Doi: 10.1016/j.enbuild.2003.10.00
Wilks, S.S. (1963). Multivariate Statistical Outliers. Sankhyā: The Indian Journal of Statistics, Series A (1961-2002). 25(4): 407-426. Disponible en: http://www.jstor.org/stable/25049292