Modelos para pronosticar series estacionales con poca información histórica: un estudio comparativo
Sergio David Madrigal Espinoza*
CIENCIA UANL / AÑO 20, No. 86 octubre-diciembre 2017
Resumen
Se investiga el desempeño de tres modelos para el pronóstico de series temporales con estacionalidad creciente y pocos datos. Dos de ellos son regresiones (una lineal con transformación Box-Cox y la otra no lineal). Estos modelos son comparados contra una alternativa autorregresiva con transformación Box-Cox. Los resultados indican que los modelos con trasformación Box-Cox pronosticarán mejor horizontes de predicción comprendidos entre uno y cuatro meses. Para horizontes mayores o iguales a cinco, el modelo de regresión no lineal será la mejor alternativa. En general, el desempeño de los modelos de regresión superará al de la alternativa autorregresiva.
Palabras clave: series temporales, modelos de regresión, pronóstico, estacionalidad y pruebas de hipótesis.
Abstract
The performance of three time series prediction models with increasing seasonality and little data is studied. Two of them are regression models (one linear with Box-Cox transformation, and the other nonlinear). The mentioned models are compared against an autoregressive model with Box-Cox transformation as an alternative. The results indicate that the models with Box-Cox transformation will better predict short time horizons, from one to four months. For longer prediction horizons, five months or more, the nonlinear regression model will be the best alternative. In general, the regression models’ performance will exceed that of the autoregressive alternative.
Keywords: time series, regression models, prediction, seasonality and hypothesis testing.
En términos estadísticos, un pronóstico es la estimación de un valor futuro. Por ejemplo, en climatología es de interés predecir la temperatura promedio para los próximos días o la precipitación pluvial, mientras que en economía, hay una gran cantidad de valores cuyo pronóstico es importante: el crecimiento, la inflación, el índice de producción industrial, etcétera.
Las empresas pueden beneficiarse de un buen pronóstico de varias formas. La estimación futura del consumo de un producto puede, por ejemplo, determinar cosas tan importantes como la expansión de una empresa; si se espera que sus clientes aumenten en número, la empresa deberá expandirse “hoy” para satisfacer la demanda de “mañana”.
Desde un punto de vista estadístico, para realizar un pronóstico se necesitan dos cosas: datos históricos y un modelo. Por ejemplo, si se desea conocer el consumo de un producto para los próximos doce meses, es necesario conocer la demanda histórica del mismo, así como un modelo que se “ajuste bien” a estos datos. Dicho modelo puede ser tan simple como una recta, sin embargo, si la demanda de este producto es afectada por las estaciones del año, el modelo a emplear debe ser más sofisticado. Cabe señalar que, entre más preciso el modelo y más datos históricos, mejores pronósticos.
Los datos son el suministro más importante para un pronóstico. Entre más hay, mejores pronósticos se pueden esperar. Esto por dos razones:
1. Los datos “sugieren” el modelo que se debe emplear para el pronóstico de los mismos. Cuando éstos son graficados respecto al tiempo, se puede deducir si son afectados o no por las estaciones del año o por el tiempo mismo o por factores macroeconómicos como la paridad peso/dólar. Entre más datos, más certeza habrá respecto a esta identificación.
2. Los datos sirven para estimar los parámetros de un modelo. Por ejemplo, si se trata de una recta, tanto su intercepto como su pendiente se estiman utilizando los datos históricos. Entre más datos, más precisa será su estimación.
Por lo anterior, cuando hay pocos datos, se dificulta obtener un buen pronóstico; no se recomienda realizar proyecciones cuando la información es escasa, razón por la cual es muy poco lo que se sabe cuando hay que predecir en esta situación.
En este trabajo se investigan los modelos que pueden ser utilizados cuando se pronostican series temporales con poca información (pocos datos históricos). En particular, se compara el desempeño de modelos de regresión frente a un modelo autorregresivo típicamente empleado en la bibliografía. El caso que se estudia es el de series temporales con estacionalidad creciente. Los modelos empleados en los cotejos son los mismos que empleó Madrigal (2014). Se utilizaron 617 series temporales para comparar estos modelos.
Los resultados indican que la efectividad de los modelos dependerá del horizonte de pronóstico. Cuando se pronostican de uno a cuatro meses, los modelos con transformación Box-Cox serán superiores. Sin embargo, para plazos mayores, la mejor opción predictiva será el modelo de regresión no lineal. En general, los modelos de regresión superarán a la alternativa autorregresiva. Contrastes de hipótesis estadísticas respaldan estas afirmaciones.
Marco Teórico y experimental
Conceptos básicos
Formalmente, una serie temporal es una secuencia de observaciones cronológicamente ordenadas. Las ventas nacionales de vehículos subcompactos por mes (figura 1) constituyen un ejemplo.
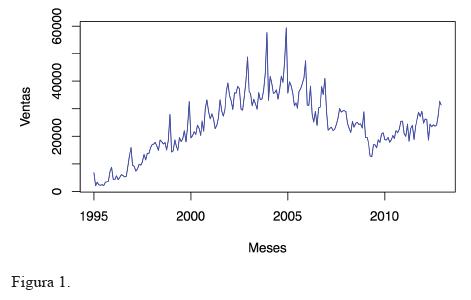
En esta serie se aprecia un crecimiento o decrecimiento atribuible a las estaciones (meses del año). Por ejemplo, las ventas máximas en cada año son alcanzadas en diciembre, mientras que las mínimas se alcanzan en abril. A este patrón se le denomina estacionalidad.
Independientemente de las estaciones del año, es posible observar que las ventas tuvieron un crecimiento constante desde 1995 hasta poco antes de 2005.
Este incremento sostenido a través del tiempo se denomina tendencia lineal. Observando toda la serie, se aprecia que ésta en general muestra una tendencia no lineal, pues no crece (o decrece) de manera constante todo el tiempo.
Note que las amplitudes de los ciclos estacionales no son constantes, sino que crecen (o decrecen) de manera proporcional a la tendencia; entre más altas las ventas, mayor es la diferencia entre los meses de abril y diciembre de cada año. Este patrón se denomina estacionalidad creciente.
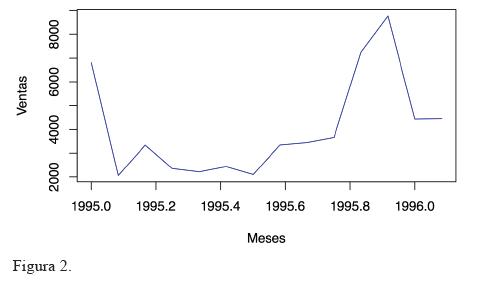
El propósito del presente trabajo es comparar el desempeño de tres modelos para el pronóstico de series temporales con tendencia no lineal y estacionalidad creciente, cuando hay muy pocos datos históricos (catorce meses). En la figura 2 se muestra un ejemplo: las ventas de vehículos subcompactos, pero esta vez, hasta febrero de 1996.
Observe que en esta fecha, resulta mucho más difícil distinguir patrones de la serie, como la estacionalidad creciente. A continuación se discuten los modelos que podrían ser empleados para la predicción de este tipo de series.
Modelos para series temporales con estacionalidad creciente
Sea yt para t = 1, …, n una serie temporal con m estaciones por periodo (meses por año [m = 12]). El índice t representa el tiempo o las etapas de la serie. Los modelos por comparar son:
1. El modelo de regresión lineal con transformación Box-Cox (MRLBC):
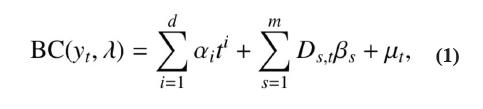
donde BC (yt , λ), representa la transformación BoxCox de la serie (Box, Jenkins y Reinsell, 2008); λ es la potencia de la transformación. Los parámetros asociados a la tendencia son αi para i = 1,…,d; d es el grado del polinomio para modelar la tendencia; βs son los parámetros asociados a las estaciones. La variable dicotómica Ds,t toma el valor uno si la estación s (s = 1, …, m) ocurre en la etapa t o cero de otro modo. Finalmente, μt es un proceso autorregresivo de orden p, μt = φ1 μt−1 + φ2 μt−2 + … + φp μt−p + εt , donde εt es un proceso de variables aleatorias independientes, normalmente distribuidas, con media cero y varianza finita y constante.
2. El modelo de regresión no lineal (MRNL):
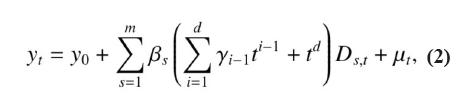
3. Los parámetros asociados a la tendencia son yi.
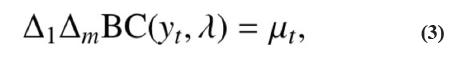
donde ∆1 yt = yt − yt −1 y ∆m yt = yt − yt−m, remueven la tendencia y la estacionalidad de la serie, respectivamente.
Diseño experimental
¿Cuál es el modelo que mejor pronostica series como la de la figura 2? Para contestar este interrogante, se emplean 617 series mensuales tomadas de la M Competition (Makridakis et al., 1982). Éstas son “recortadas” para simular información escasa. Los modelos son estimados utilizando únicamente las primeras catorce observaciones de cada serie y se pronostican los próximos 18 meses.
Para cada horizonte de pronóstico, se obtiene una medida de error denominada desviación porcentual absoluta (DPA), definida de la siguiente manera:
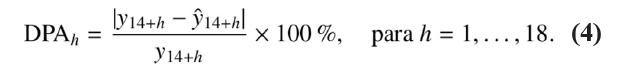
donde ![]() 14+h representa el pronóstico realizado en el tiempo t = 14 para h etapas adelante, mientras que y14+h representa el dato real del conjunto de prueba.
14+h representa el pronóstico realizado en el tiempo t = 14 para h etapas adelante, mientras que y14+h representa el dato real del conjunto de prueba.
Para cada h y para cada modelo, el promedio del estadístico DPAh sobre las 617 series es acomodado en un cuadro cuyas columnas corresponden a los modelos. Para determinar si las diferencias entre éstos son significativas, se utiliza la prueba ANOVA de dos factores; el otro factor son los horizontes de pronóstico (renglones) y se supone que influyen en el resultado.
Una vez que se determina que las diferencias entre los modelos no se deben al azar, es necesario comparar cada par de modelos para saber cuál o cuáles son significativamente diferentes. Para realizar estas comparaciones se utiliza la prueba de Tukey (Miller, 1981; Yandell, 1997). Todo fue hecho utilizando GNU R (R Core Team, 2016), un programa de análisis estadístico 100% gratuito y de código abierto (Hyndman, 2012). El nivel de significación utilizado durante las pruebas es α = 0.05. Debido a la escasez de información, se supuso que μt = εt.
Resultados
En la tabla I se muestran, para cada valor de h y para cada modelo, los resultados del estadístico DPA promediados sobre las 617 series. En la figura 3 se muestra gráficamente esta información.
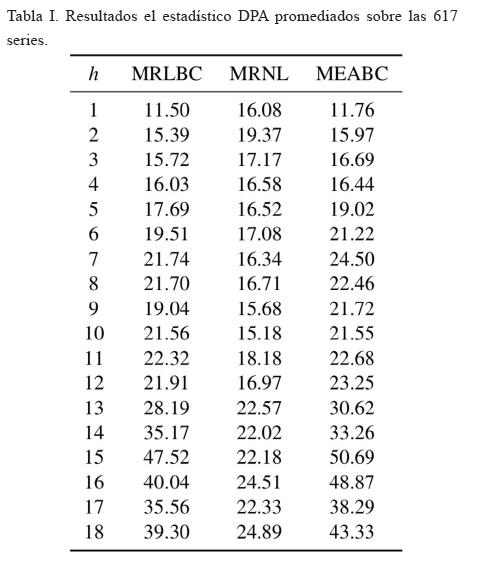
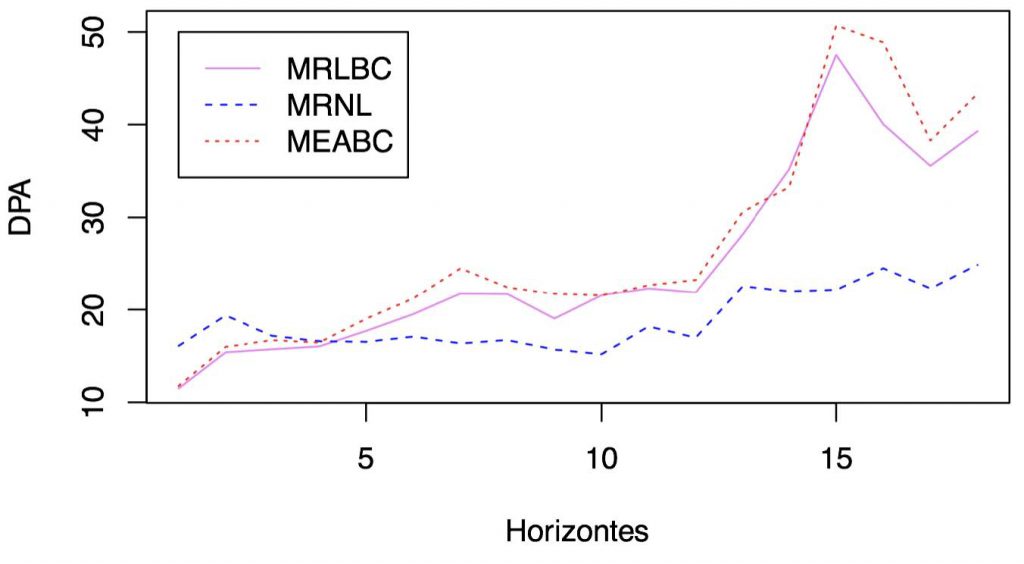
Figura 3. Representación gráfica de la tabla I.
Las medias de las columnas de la tabla I son MRLBC = 24.99, MRNL = 18.91 y MEABC = 26.8. Al aplicar la prueba ANOVA, aislando el efecto de los renglones, se obtiene un p–valor de 0.0000714, por lo que se concluye que los modelos son significativamente diferentes. La prueba de Tukey encuentra diferencias significativas entre el MRNL y los modelos MRLBC y MEABC con p-valores de 0.0019879 y 0.0000830, respectivamente. No hubo diferencias significativas entre los últimos dos modelos mencionados.
Discusión
La prueba ANOVA concluye lo que parecía evidente: los modelos son estadísticamente diferentes. Esto conduce a las comparaciones de Tukey para cada par de modelos. Puesto que la media del MRNL es inferior a la de los otros dos, se concluye que éste es el mejor modelo cuando hay escasa información. Sin embargo, aunque esto se cumpla para los dieciocho meses pronosticados, no se cumple para los primeros cuatro, en los que es evidente según la figura 3, que los modelos con transformación Box-Cox, y en especial el MRLBC, mostrarán un desempeño superior. Las medias de los modelos de regresión son menores a las del modelo autorregresivo. Esto índica que los modelos de regresión son mejores, aunque sólo uno de ellos lo es de manera significativa.
Conclusiones
Se pronosticaron 617 series temporales estacionales con escasa información. Se utilizaron tres modelos, dos de regresión y uno autorregresivo. Se emplearon contrastes de hipótesis estadísticas para detectar diferencias significativas en el desempeño predictivo de los modelos.
Los resultados son contundentes: el MRNL ofrecerá, en promedio, el mejor desempeño de pronóstico para horizontes entre uno y dieciocho meses. Sin embargo, para periodos inmediatos de pronóstico, que comprenden entre uno y cuatro meses, los modelos con transformación Box-Cox, en especial el MRLBC, ofrecerán un mejor desempeño.
En general, el desempeño de los modelos de regresión parece superar al del modelo autorregresivo cuando hay poca información. Éste es un resultado que no había sido reportado antes y sienta un precedente favorable para estos modelos.
Se recomienda, a quienes deben pronosticar series temporales estacionales con pocos datos, seguir estas recomendaciones para minimizar los errores en sus proyecciones y, de esta manera, tomar mejores decisiones.
* Universidad Autónoma de Nuevo León
Referencias
Box, G.E.P., Jenkins, G.M., y Reinsell, G.C. (2008). Time series analysis: Forecasting and Control. EE.UU.:WILEY.
Hyndman, R.J. (2012). Mcomp: Data from the M-competitions, Disponible en: http://CRAN.R-project.org/package=Mcomp. R package version 2.04
Madrigal E., S.D. (2014). Modelos de regresión para el pronóstico de series temporales con estacionalidad creciente. Computación y Sistemas, 18(4):821–831, 12 doi: 0.13053/CyS-18-4-1552. URL http: //dx.doi.org/0.13053/CyS-18-4-1552.
Makridakis, A.S., et al. (1982). The accuracy of extrapolation (time series) methods: Results of a forecasting competition. Journal of Forecasting, 1(2):111-153.
Miller, R.G. (1981). Simultaneous Statistical Inference. Nueva York: Springer/Verlag.
R Core Team. (2016). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Disponible en: https://www.r-project.org/
Yandell, B.S. (1997). Practical Data Analysis for Designed Experiments. Florida:Chapman & Hall.
Recibido: 04/07/2016
Aceptado: 03/07/2017
