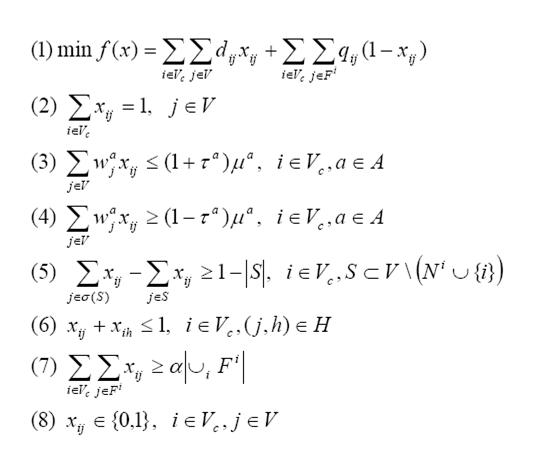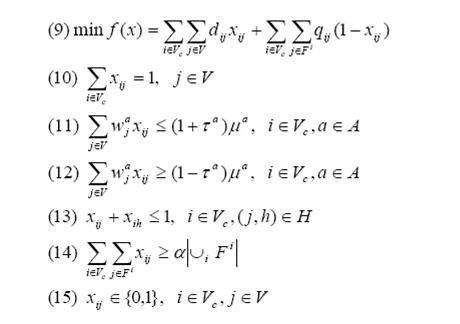Planificación inteligente de territorios comerciales bajo requerimientos de realineación y asignación disjunta
ROGER Z. RÍOS MERCADO*, J. FABIÁN LÓPEZ PÉREZ*
CIENCIA UANL / AÑO 18, No. 71, ENERO-FEBRERO 2015
El agrupamiento de pequeñas áreas geográficas en zonas más grandes (clusters), de acuerdo a criterios establecidos, se denomina en la bibliografía especializada territorio o distrito. En la investigación de operaciones, el primer trabajo publicado para el problema de diseño y planificación de territorios puede ser referenciado a Forrest (1) y Hess et al., (2) respectivamente. Dependiendo del contexto del problema de aplicación, el concepto de “diseño territorial” se utilizaría como una equivalencia al concepto de “distritación”, que tanto se conoce en el ámbito de la demografía geopolítica.
La investigación en el área de “distritación” es verdaderamente multidisciplinaria, ya que incluye muchos campos: la geografía, la ciencia política, la administración pública y, por supuesto, la investigación de operaciones. Sin embargo, todos estos problemas tienen en común la tarea de subdividir la región bajo estudio para el diseño y planificación de un cierto número de territorios, considerando diversos aspectos de capacidad. De hecho, los problemas de diseño territorial emergen de diversos tipos de aplicaciones del mundo real. Por mencionar algunos, podemos citar las aplicaciones de distritación política o electoral, (3,4) el diseño de territorios para maximizar el aprovechamiento de la fuerza de ventas, (5-9) la distritación escolar10 y, por supuesto, el diseño territorial comercial,11-17 que es la aplicación de interés en el presente trabajo. El lector podrá encontrar una amplia discusión de trabajos de diseño territorial en Duque et al. (18) y Kalcsics et al. (19) La mayoría de los servicios públicos, incluidos hospitales, escuelas, el transporte urbano, el correo postal, etc., se administra sobre supuestos de límites territoriales. Aspectos económicos o también demográficos deben tomarse en consideración para el diseño y planificación de territorios equilibrados que luego se traducen en aspectos de eficiencia económica y nivel de servicio.
Como ejemplo de lo anterior, si suponemos que cada uno de los territorios obtenidos en un plan óptimo es administrado por un solo recurso, tiene sentido entonces la aplicación de criterios de balanceo para la cantidad de clientes, el volumen de ventas, las comisiones otorgadas, los recorridos en tránsito y las jornadas de trabajo asignados a cada responsable territorial. Finalmente, es importante considerar ciertas restricciones físicas como parte de la definición geográfica del problema. Nos referimos a las características de contigüidad y de compacidad que deben tener los territorios obtenidos como resultado del diseño óptimo.
El presente desarrollo se aplicó para el diseño y planificación de los territorios de venta y atención comercial de la red metropolitana de distribución de bebidas embotelladas de la empresa Embotelladoras ARCA, en la ciudad de Monterrey, N.L. Esta distribución consiste en la entrega y recolección física de producto desde los centros de distribución hacia los clientes finales, autoservicios, tiendas de conveniencia, supermercados, restaurantes, tiendas de abarrotes, etc. El 90% del modelo de distribución de Embotelladoras ARCA se basa en un modelo de preventa terciada, esto es, se levanta el pedido hoy y se entrega al día siguiente.
Cada ruta atiende un rango de 70 a 85 clientes por día. De este conjunto de clientes a ser atendidos por cada ruta de reparto, estadísticamente se conoce que hasta 40% de éstos requiere atención dentro de cierta ventana de servicio (restricciones de horario). Adicionalmente, Embotelladoras ARCA opera rutas fijas de distribución a lo largo de todo el año, independientemente de la curva de estacionalidad. Es fácil identificar que, potencialmente, existen fuentes de inequidad en las cargas de trabajo de cada ruta a lo largo del año.
El proceso de diseño y planificación de rutas actualmente se define en forma manual y empírica. Lo anterior limita la posibilidad de operar con mejores esquemas que generen beneficios económicos por reducción de costos; asimismo, ocasiona un gasto innecesario y justifica el requerimiento de nuestro proyecto.
El desarrollo del proyecto obedece a una necesidad real y general que se presenta en la industria embotelladora y distribuidora de bebidas. La enorme demanda de un producto muy atomizado y de uso cotidiano da como resultado que a la red de distribución la forme un número considerable de puntos de venta. Por tanto, las entidades geográficas a agrupar y planificar son del orden de varias decenas de miles de elementos. La industria en general ha encontrado que dividir estos puntos en pequeños territorios, diseñados bajo criterios económicos y geográficos bien definidos, hace posible la administración de este enorme número de entidades económicas. Así, entonces, los camiones repartidores son asignados para atender a uno o varios grupos (distritos, territorios) y sus rutas se diseñan considerando sólo los clientes ubicados en cada territorio.
Los objetos que se busca agrupar son los puntos de venta, pero, dado su enorme número, se ha hecho un primer agrupamiento a fin de reducir la escala del problema y simplificar su solución. Así, entonces, todos los puntos de venta ubicados en una misma manzana geográfica se consideran como uno solo. De forma que el objeto básico a planificar para el diseño de los territorios será entonces el conjunto de las manzanas geográficas de la ciudad de Monterrey (aproximadamente 34 mil manzanas). Con cada punto de venta se asocian varias medidas de desempeño (variables de actividad), y estas mismas tasas de rendimiento se asocian con cada manzana geográfica definida. Para cada manzana física, las medidas de desempeño serán simplemente la suma aritmética de las medidas correspondientes de los puntos de venta que la conforman.
El entregable del proyecto es un modelo matemático (software) diseñado para resolver de manera eficiente y efectiva problemas de diseño y planificación de territorios. El software está diseñado para realizar análisis geoespaciales de información de mercado de manera combinatoria a través del empleo de variables demográficas y socioeconómicas. Se busca impactar económicamente en la rentabilidad operativa y en el servicio dedicado a la distribución secundaria de Embotelladoras ARCA.
Descripción del problema
El problema para el diseño y planificación óptima de territorios se puede definir como el proceso para agrupar áreas básicas, es decir, manzanas geográficas, en grupos o clusters geográficos de mayor tamaño. Estos nuevos clusters geográficos se denominan territorios. El planteamiento del problema incluye que cada manzana básica puede estar asignada a un solo territorio. El número de los territorios p que se requiere es conocido y está determinado como un parámetro del modelo. Por otra parte, se requiere cubrir los criterios de compacidad y de contigüidad para los territorios propuestos en el plan óptimo. El atributo de contigüidad se definiría como el efecto deseado de asegurar que un territorio no esté deformado geográficamente. Lo anterior se traduce en que las manzanas geográficas que conforman un territorio tengan que estar geográficamente conectadas entre sí, y no dispersas. Es fácil entender que para obtener territorios contiguos, la información geográfica de las fronteras (o vecindades) de cada manzana debe ser explícitamente alimentada al modelo matemático.
Los territorios compactos, por lo general, tienen una operación geográficamente concentrada, lo cual permite disminuir los tiempos muertos por trayecto y, por tanto, incrementar el tiempo disponible para el mejor nivel de servicio.
En las aplicaciones de diseño territorial del mundo real, las variables de balanceo que principalmente han sido utilizadas, están asociadas de manera directa a la actividad de venta en sí misma. La definición de nuestro problema incluye tres variables cuantificables para cada manzana básica. Utilizaremos tres variables de actividad para cada manzana básica: (i) cantidad de clientes, (ii) volumen de ventas y (iii) jornada de trabajo. La jornada de trabajo se define como la cantidad de tiempo que cada punto de venta (cliente) requiere, esto incluye tiempo de traslado, entrega de mercancía, recolección de envases y limpieza de exhibidores. Dicha variable de actividad es muy dependiente del tipo de servicio ejecutado en el punto de venta, lo cual a su vez depende de las características de cada cliente, así como de su localización geográfica.
La variable de actividad de un territorio se define como la suma aritmética de la variable de actividad del total de las manzanas básicas que conforman dicho territorio. El diseño óptimo busca que todos los territorios construidos estén apropiadamente equilibrados. De hecho, este procedimiento de balanceo es considerando cada una de las tres variables de actividad de manera individual y simultánea. Las manzanas básicas son entes geográficos con una ubicación específica en una región. Los territorios formados toman en cuenta esta ubicación natural, y es requisito que el territorio se forme únicamente con manzanas que colindan entre sí. Hay una razón muy simple detrás de esto. Si para llegar a algún punto de venta (manzana) es necesario que el camión atraviese por puntos de venta que no pertenecen a su distrito, la reacción de los clientes, al verlo en sus alrededores, será pedirle abasto de mercancía. El repartidor no traerá más abasto que el calculado para su programación, por lo que el servicio tendría que negarse. Esto tiene como resultado que el cliente perciba una mala atención de su proveedor. Lo anterior deteriora la imagen de la empresa y constituye una fuente potencial de daño económico.
La definición de nuestro problema incluye algunos diseños de territorios prescritos o prohibidos. Eso significa que algunas manzanas básicas por definición deban estar asignadas a un territorio específico. Del mismo modo habría el caso contrario en el que ciertas manzanas básicas no pudieran estar asignadas conjuntamente a un territorio específico. Todas estas características se pueden fácilmente aprovechar para que el modelo considere, como parte de la definición del problema, algunos territorios ya predeterminados de manera parcial desde el principio del proceso de planeación, como resultado de experiencias o planes anteriores. Eso significa que nuestro modelo puede tomar en consideración ciertos territorios ya existentes, y a partir de ahí asignar el resto de las manzanas básicas a dichos territorios preconstruidos.
De manera especial, estas características del modelo se pueden también aplicar para considerar los obstáculos geográficos, como ríos y montañas. Generalizamos entonces que nuestro problema de diseño territorial es común a todas aquellas aplicaciones del mundo real en las que se opere con un grupo de recursos escasos, y que éstos requieran asignarse para subdividir un área geográfica extensa de trabajo en subregiones de responsabilidad equilibradas. El objetivo entonces es encontrar el mejor agrupamiento por medio del cual se satisfagan las restricciones impuestas, y al mismo tiempo lograr la formación de grupos (distritos) balanceados con respecto a ciertos parámetros de venta y distribución establecidos.
El problema se resume como sigue: agrupar un conjunto V de manzanas básicas (con tres atributos de actividad en cada manzana) en un número limitado de p territorios que satisfagan los criterios especificados de balance para cada actividad, compacidad, contigüidad y similitud con el plan anterior. El problema se modela como un problema de programación entera mixta lineal. (20)
Método de solución propuesto
En esta sección presentamos la estrategia de solución para resolver el modelo de asignación (AM). Considérese el modelo AM desplegado en las expresiones (1)-(8), donde V denota el conjunto de unidades básicas (UBs); Vc el conjunto de centros territoriales; A el conjunto de atributos de las UBs; Fi el conjunto de UBs preespecificadas asociadas al centro territorial i del plan existente; dij, la distancia entre unidades i y j en V; H el conjunto que contiene todos los pares de manzanas que deben asignarse a territorios diferentes; wi a el valor de la actividad a ∈ A (número de clientes, demanda de producto y carga de trabajo) en el nodo i; τa el parámetro de tolerancia de la actividad a; μa tamaño promedio del terriorio a, dado por μa = Σi∈v wai / p el conjunto de nodos que son adyacentes al nodo i. Las variables binarias de decisión se definen como xij = 1, si la UB j se asigna al territorio con centro en i; =0, de otro modo.
Modelo (AM)
Una de las dificultades principales en la resolución de este modelo es el número exponencial de restricciones de conectividad en (5), lo cual implica que es prácticamente imposible escribirlas explícitamente.
Por lo tanto, consideramos en su lugar el modelo relajado (AMR) de (AM), el cual consiste básicamente de relajar estas restricciones de conectividad (5) del Modelo AM.
Modelo (AMR)
La idea fundamental de nuestro método propuesto es resolver el modelo AMR, como un programa entero mixto, y luego verificar si la solución obtenida satisface las restricciones de conectividad. Si las satisface, la solución obtenida para el AMR resuelve también el AM. Si no, se determinan cuáles restricciones de conectividad no se satisfacen. Para determinar esto, se resuelve un problema de separación bastante sencillo, se generan las restricciones violadas y se agregan al modelo AMR. El procedimiento se repite iterativamente hasta que la solución obtenida es totalmente conexa, lo cual implica una solución óptima al modelo AM. Esto se garantiza porque el problema de separación que identifica las restricciones o cortes que no se satisfacen se resuelve de forma exacta y además muy eficientemente. Una panorámica general del método se despliega en la figura 1.
En el paso 1 se usa un método de ramificación y acotamiento, dado que no estamos relajando la condición de integralidad de las variables binarias. Esta técnica es motivada por el hecho de que el modelo AMR puede resolverse óptimamente por métodos actuales de ramificación y acotamiento relativamente rápido para instancias grandes. Por ejemplo, el modelo AMR puede resolverse en aproximadamente 30 seg. de CPU en una PC en instancias de 5000 nodos. Además, el identificar y generar las restricciones o cortes violados en el paso 2 puede efectuarse de manera eficiente en tiempo polinomial, de tal forma que el procedimiento de solución visto globalmente parece atractivo siempre y cuando el número de iteraciones requeridas para converger y alcanzar optimalidad no sea muy grande. El algoritmo encuentra una solución al modelo AM.
Existen varios puntos importantes en materia de investigación de particular interés. Un tema importante es investigar el comportamiento empírico del método propuesto en términos del número de iteraciones/cortes requeridos para converger al óptimo. Además, el hecho de que suponemos un conjunto dado de centros nos lleva a investigar si podemos explotar este hecho para desarrollar varias estrategias algorítmicas de solución que permitan acelerar la convergencia del método.
Estrategias algorítmicas para acelerar convergencia
1. Fijando variables: eliminación de asignaciones de manzanas relativamente lejanas.
2. Fijando variables: preasignación de manzanas relativamente cercanas.
3. Fortaleciendo las restricciones de conectividad.
4.- Encontrando desigualdades violadas. (20)
Trabajo experimental
En esta sección presentamos una evaluación completa del método de solución, así como de cada uno de sus componentes y estrategias desarrolladas. El tema central consiste en investigar el costo-beneficio de las estrategias implementadas y mostrar su valoración científica y práctica. El modelo fue implementado en el optimizador de programas enteros mixtos X-PRESS de FICOTM (Fair Isaac, antes conocido como Dash Optimization). El método fue ejecutado en una PC con dos procesadores Intel Core, a una velocidad de 1.4GHz, bajo el sistema operativo Win X64. Para evaluar el método propuesto, usamos algunas instancias reales de 5000 y 10000 nodos y 50 territorios. En todos los experimentos, usamos ta = 0.10 para toda a ∈ A, y un intervalo de optimalidad relativa de 0.01% como criterio de paro.
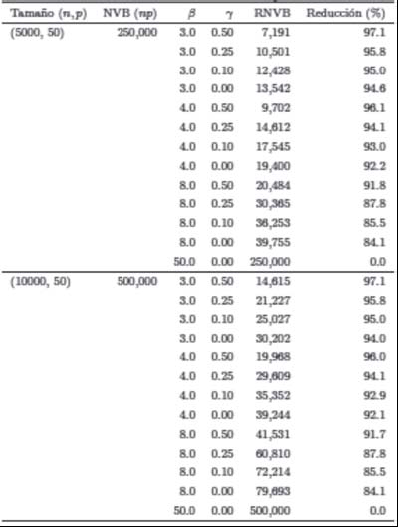
La tabla I muestra el efecto de cómo se reduce el tamaño del problema bajo diferentes valores de los parámetros introducidos en la sección 5. Las primeras dos columnas reflejan el tamaño de la instancia original en términos de su número de UBs, número de territorios y número de variables binarias (NBV). La tercera y cuarta columna despliegan los valores de los parámetros β y γ empleados en cada ejecución, respectivamente. La quinta columna (RNVB) muestra el número de variables binarias después de la reducción. La última columna muestra la reducción relativa lograda con respecto al tamaño original dada por 100 × (NBV -RNBV)/NBV. Como puede apreciarse, el número de variables binarias en el problema reducido crece a medida que β crece y γ decrece. Nótese que el caso β= 50.0 y γ= 0.0 implica que no se aplica ninguna reducción.
Resumiendo, la estrategia que adoptamos es disminuir el espacio de soluciones factibles (para hacer el problema más tratable), para abordar un problema reducido que puede resolverse más eficientemente sin una pérdida significativa de optimalidad. Ahora procedemos precisamente a investigar este costo-beneficio. Ahora procedemos a aplicar nuestro método a instancias de 5000 UBs con 50 territorios. En este experimento fijamos ˜γ= 0.0, es decir, no aplicamos la estrategia de conectividad forzada. La meta de este experimento es evaluar el costo-beneficio entre calidad de solución y tiempo de cómputo para diferentes valores de β y γ.
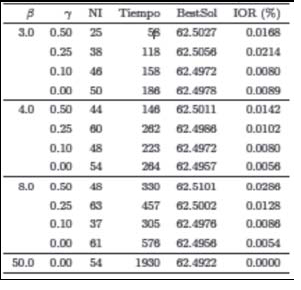
La tabla II muestra los resultados. Las primeras dos columnas indican los valores de β y γ utilizados. La tercera y la cuarta columnas muestran el número de iteraciones (NI) y tiempo de CPU (seg.). La quinta columna despliega el valor de la mejor solución factible encontrada (BestSol), y la última columna muestra el intervalo de optimalidad relativa (IOR) entre esta solución y la solución óptima (que corresponde a la fila β= 50.0 y γ= 0 cuando no se aplica ninguna reducción).
Como se aprecia en la tabla, los resultados son realmente impactantes. La calidad de los resultados es excelente: reporta desviaciones del óptimo menores a 0.03%, en menos de seis minutos en todos los casos. Nótese que la estrategia reportada en la primera fila (correspondiente al caso β= 3.0 y γ= 0.50) tomó menos de un minuto, reportó una solución que está a menos de 0.02% del óptimo global, lo cual es impactante. La solución óptima (última fila) se obtuvo en poco más de 30 minutos de CPU. En resumen, esto muestra que con las estrategias adoptadas es posible encontrar soluciones casi óptimas en unos cuantos segundos de tiempo, y lograr reducciones de tiempo de cómputo considerables.
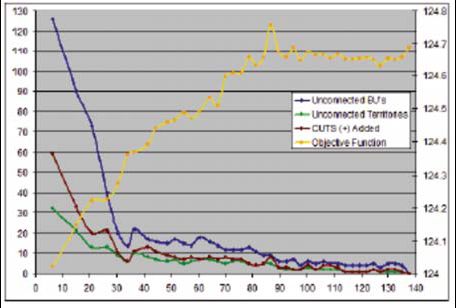
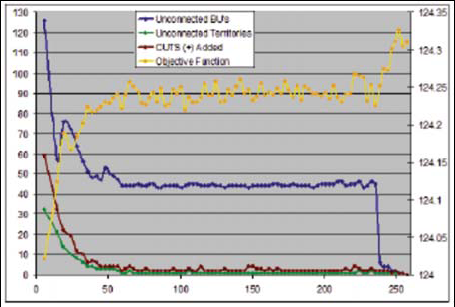
A continuación, procedemos a ilustrar el desempeño interno del método como función del tiempo, a través de las iteraciones del algoritmo. Las figuras 2 y 3 muestran los resultados para dos casos diferentes con valores (β,γ,δ) de (3.0, 0.25, 50.0) y (3.0, 0.25, 25.0), respectivamente. En cada figura graficamos las siguientes medidas: (i) número de UBs desconexas, (ii) número de territorios desconexos, (iii) número de cortes agregados, y (iv) valor de la función objetivo como función de las iteraciones, las cuales se muestran en el eje horizontal. Las medidas (i)-(iii) se miden en el eje vertical izquierdo y la medida (iv) en el eje vertical derecho.
Se aprecia que, en la figura 2, las primeras dos ejecuciones con alto valor del parámetro tienen un comportamiento similar. El número de UBs desconexas, de territorios deconexos y de cortes agregados al modelo decrecen con el número de iteraciones. Algo similar ocurre con el valor de la función objetivo, pero en sentido opuesto. En los otros dos casos (figura 3), con valor bajo de δ, se presenta un comportamiento muy diferente. Particularmente, el valor de la función objetivo se mueve lentamente conforme avanza el tiempo. En efecto, esta es la razón por la cual se obtienen valores bajos en la función objetivo. De ambos modos, es importante señalar que nuestra metodología presenta un modelo entero que asegura asignaciones enteras en cada iteración. Por tanto, resulta relevante verificar que tan rápido nuestra heurística, implementada para el modelo entero de asignación evoluciona, y converge en soluciones con un alto grado de conectividad.
Finalmente, la figura 4 despliega la solución gráfica de la instancia de 5000 UBs, 50 territorios con tolerancia de 0.05. La leyenda en el costado del grafo indica el número de UBs contenidas en cada territorio, el cual se identifica por un código de color diferente.
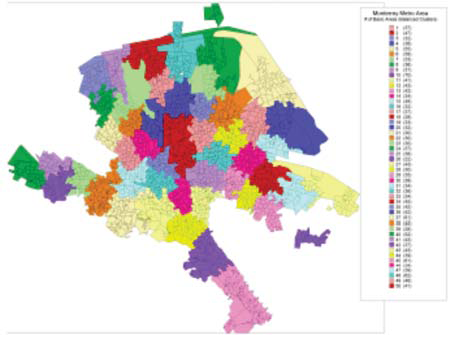
Fig. 4. Resultado geográfico de un diseño territorial óptimo de la ciudad de Monterrey con 5000 UBs.
CONCLUSIONES
Encontramos diversos enfoques en la investigación de operaciones que han sido propuestos para dar tratamiento al problema de diseño territorial, algunos basados en programación mixta entera, otros en heurísticas y otros más en metaheurísticas. En general, este problema está catalogado como matemáticamente difícil de resolver (NP-duro) y, por tanto, no es trivial su tratamiento para solucionar instancias de gran escala. Nuestro algoritmo computacional se enfoca en resolver eficientemente este tipo de problemas.
Se detalló la metodología, así como algunos resultados computacionales obtenidos durante la experimentación. Los resultados son satisfactorios en la parte computacional y económica. Nuestra metodología puede extenderse para dar tratamiento a muy diversas variables de actividad simultáneamente. Lo anterior permite incorporar diferentes reglas de negocio y criterios de planeación. Como beneficio directo de la estrategia metodológica empleada, podemos reducir significativamente la complejidad matemática del problema, dependiendo del nivel de detalle y agregación que se requiera manejar en un problema de aplicación real. Resulta evidente la conveniencia de integrar este tipo de modelos matemáticos en los sistemas de información geográficos (GIS), con la finalidad de brindar al usuario final mayor soporte en la toma de decisiones relacionadas con el diseño y planificación de territorios. En general, los problemas de distritación y diseño territorial son de naturaleza multidisciplinaria y, por tanto, muy dependientes del contexto de aplicación, lo cual determina cuáles criterios deben verse como restricciones a cubrir y cuáles como objetivos a optimizar.
La aplicación directa de la propuesta tecnológica para la operación de embotelladoras ARCA se traduce en una mayor eficiencia en el aprovechamiento del equipo de transporte y, en general, en la minimización del costo operativo de la distribución secundaria. El software propuesto considera las restricciones de ventana de horario de los clientes para el óptimo diseño territorial. Lo anterior se traduce en un beneficio directo en el incremento de efectividad en la entrega de los pedidos al cliente y en una reducción en los trayectos muertos que se recorren en el territorio.
Por este conducto, se puede asegurar que la atención de una mayor cantidad de clientes en un menor tiempo y con el menor uso de recursos, lo cual redunda directamente en el beneficio económico del costo en la operación del negocio de distribución. Con lo anterior, se logra una posición más estratégica en la distribución del producto, con una diferenciación en comparación con los procesos de la competencia y obtener con ello una clara ventaja competitiva en costo, cobertura y nivel de servicio. Las ventajas competitivas creadas por este desarrollo permiten la explotación de información detallada por área territorial, con el fin de establecer estrategias de mercado ya no de manera general, sino definiendo oportunidades por segmento demográfico para maximizar el aprovechamiento, tanto de los activos fijos como de las oportunidades de mercado. La utilidad económica que la propuesta ofrece es altamente significativa para cualquier empresa que cuente con un proceso de distribución. Se estima reducir el costo de distribución alrededor de 5%. Este potencial pudiera aprovecharse alternativamente para que el exceso de capacidad de transporte sirva para incrementar el nivel de cobertura en la distribución (incremento en el volumen de venta).
Dadas las características de distribución de ARCA, nuestra propuesta tecnológica resulta estratégica y altamente influyente en la obtención de los resultados del negocio. El desarrollo de tecnología propia sienta las bases en materia de distribución, y es punto de partida de nuevos e innovadores desarrollos en la materia, lo cual permitirá que ARCA genere ventajas competitivas que tengan una incidencia directa en los costos y la rentabilidad del negocio. Por sus ventajas tecnológicas y potencialidad para planificar adecuadamente el mercado, la empresa califica al proyecto como de beneficio económico y social, además de rentable, ya que se logra la recuperación de la inversión en el primer año.
La realización de este tipo de desarrollos tecnológicos brinda ventajas competitivas, ya que arroja beneficios que se reflejan en diversas áreas de la organización: mejor manejo de los activos de la empresa, desarrollo de mercados, estrategias de segmentación por territorio, administración de precios y promociones, planeación de la cadena de suministro, administración de márgenes de utilidad por canal, etc. Lo anterior implica un incremento en la rentabilidad para la empresa. Esto es cierto, ya que al tener una flota de distribución más eficiente, disminuye el requerimiento de inversión en unidades antiguas por efecto de su reposición, lo que a su vez habilita la oportunidad de invertir en nuevas áreas productivas del negocio.
RESUMEN
El diseño y planificación de territorios se define como el problema que se enfoca en la agrupación de áreas geográficas básicas, en grupos o “clusters” geográficos, con una extensión geográfica o demográfica mayor. Estos clusters se pueden referir como territorios. En este artículo consideramos el problema en que tres variables (o atributos de actividad) deben tomarse en consideración para construir un diseño y plan óptimo de balanceo territorial (o también denominado distritación). Cada variable de actividad tiene una métrica definida y específica (por ejemplo, cantidad de clientes, volumen de ventas, jornadas de trabajo, etc). Adicionalmente existen restricciones geográficas relacionadas a la contigüidad y la compacidad (compacto) para cada uno de los territorios que se construyen como resultado del proceso de diseño y planeación. Se obtiene un diseño y plan territorial óptimo cuando los territorios resultantes quedan balanceados lo mejor posible y de manera simultánea para cada una de las variables de actividad consideradas por el tomador de decisiones. Matemáticamente, este problema es difícil de resolver (NP-duro).
Nuestra metodología (algoritmo) da tratamiento al problema a través de un modelo de programación mixta entera (Mixed Integer Programming, MIP). Nuestra implementación fue probada y puesta en práctica para instancias de gran escala para más de 10000 manzanas geográficas. Algunas métricas sobre eficiencia computacional y conveniencia económica se presentan con resultados favorables.
Palabras clave: Investigación de operaciones, Diseño de territorios, Programación lineal entera mixta, Desigualdades válidas, Ramificación y acotamiento.
ABSTRACT
Territory design or districting can be defined as the problem of partitioning a set of basic units into clusters or territories. In this paper, we address a commercial territory design problem subject to planning requirements such as multiple territory balancing, compactness, connectivity, disjoint assignment, and similarity with existing plan. Mathematically speaking, this problem is difficult to solve (NP-Hard). A mixed-integer linear programming model is introduced for this problem. Given its complexity, a novel technique based on branch-and-bound and cut generation is proposed for solving the problem. The method is enhanced by several algorithmic strategies.
The empirical assessment of the proposed procedure shows its excellent performance by finding optimal and near-optimal solutions to very largescale real-world instances in a few minutes of computational effort.
Keywords: Operations research, territory design, Mixed-integer linear integer programming, Valid inequalities, Branch and bound.
Agradecimientos
Este trabajo de investigación ha sido financiado por el Conacyt (apoyos CB05-01-48499-Y y CB11-01-166397) y por el Paicyt de la UANL (apoyos CE012- 09, CS470-10, IT511-10, CE728-11, HU769-11).
* Universidad Autónoma de Nuevo León.
Contacto: roger@yalma.fime.uanl.mx
————————
El presente artículo está basado en la investigación “Planificación inteligente de territorios comerciales incluyendo requerimientos de realineación y asignación disjunta”, galardonado con el Premio de Investigación UANL 2014 en la categoría de Ciencias Exactas, otorgado en sesión solemne del Consejo Universitario de la UANL, en agosto de 2014.
Referencias
1. E. Forrest. Apportionment by computer. American Behavioral Scientist, 8:23–35, 1964.
2. S.W. Hess, J.B. Weaver, H.J. Siegfeldt, J.N. Whelan y P.A. Zitlau. Nonpartisan political redistricting by computer. Operations Research, 13(6):998–1006, 1965.
3. M.H. Browdy. Simulated annealing: An improved computer model for political redistricting. Yale Law and Policy Review, 8:163–179, 1990.
4. S.W. Hess, J. B. Weaver, H. J. Siegfeldt, J. N. Whelan y P. A. Zitlau. Nonpartisan political redistricting by computer. Operations Research, 13(6):998–1006, 1965.
5. A. Drexl y K. Haase. Fast approximation methods for sales force deployment. Management Science, 45(10):1307–1323, 1999.
6. A.A. Zoltners. A unified approach to sales territory alignment. En R. P. Bagozzi, editor, Sales Management: New Developments from Behavioral and Decision Model Research, pp. 360–376. Marketing Science Institute, Cambridge, Inglaterra, 1979.
7. A.A. Zoltners y S.E. Lorimer. Sales territory alignment: An overlooked productivity tool. Journal of Personal Selling and Sales Management, XX(3):139–150, 2000.
8. A.A. Zoltners y P. Sinha. Sales territory alignment: A review and model. Management Science, 29(11):1237–1256, 1983.
9. A.A. Zoltners y P. Sinha. Sales territory design: Thirty years of modeling and implementation. Marketing Science, 24(3):313–331, 2005.
10. F. Caro, T. Shirabe, M. Guignard y A. Weintraub. School redistricting: Embedding GIS tools with integer programming. Journal of the Operational Research Society, 55(8):836–849, 2004.
11. R.Z. Ríos-Mercado y E. Fernández. A reactive GRASP for a commercial territory design problem with multiple balancing requirements. Computers & Operations Research, 36(3):755–776, 2009.
12. R.Z. Ríos-Mercado y J.C. Salazar-Acosta. A GRASP with strategic oscillation for a commercial territory design problem with a routing budget constraint. En I. Batyrshin y G. Sidorov, editores, Advances in Soft Computing, volumen 7095 de Lecture Notes in Artificial Intelligence, pp. 307–318. Springer, Heidelberg, Alemania, 2011.
13. M.A. Salazar-Aguilar, R.Z. Ríos-Mercado y M. Cabrera- Ríos. New models for commercial territory design. Networks & Spatial Economics, 11(3):487–507, 2011.
14. M.A. Salazar-Aguilar, R.Z. Ríos-Mercado y J.L. González- Velarde. A bi-objective programming model for designing compact and balanced territories in commercial districting. Transportation Research Part C: Emerging Technologies, 19(5):885–895, 2011.
15. M.A. Salazar-Aguilar, R.Z. Ríos-Mercado y J.L. González-Velarde. GRASP strategies for a bi-objective commercial territory design problem. Journal of Heuristics, 19(2):179–200, 2013.
16. M.A. Salazar-Aguilar, R.Z. Ríos-Mercado, J.L. González-Velarde y J. Molina. Multiobjective scatter search for a commercial territory design problem. Annals of Operations Reseach, 199(1):343-360, 2012.
17. L. Vargas-Suárez, R.Z. Ríos-Mercado y F. López. Usando GRASP para resolver un problema de definición de territorios de atención comercial. En M. G. Arenas, F. Herrera, M. Lozano, J. J. Merelo, G. Romero y A. M. Sánchez, editores, Actas del IV Congreso Español en Metaheurísticas y Algoritmos Evolutivos y Bioinspirados (MAEB), pp. 609–617, Granada, España, Septiembre 2005.
18. J.C. Duque, R. Ramos y J. Suriñach. Supervised regionalization methods: A survey. International Regional Science Review, 30(3):195–220, 2007.
19. J. Kalcsics, S. Nickel y M. Schroder. Towards a unified territorial design approach: Applications, algorithms, and GIS integration. TOP, 13(1):1–56, 2005.
20. R.Z. Ríos-Mercado y J.F. López-Pérez. Commercial territory design planning with realignment and disjoint assignment requirements. Omega, 41(3):525-535, 2013.
Recibido: 18/07/14
Aceptado: 18/08/14