PROPIEDADES FÍSICAS DEL MESÓN SIGMA EN EL VACÍO
José Rubén Morones Ibarra*, Mónica del Carmen Menchaca Maciel*
CIENCIA UANL / AÑO 22, No.96 julio-agosto 2019
https://doi.org/10.29105/cienciauanl22.96-2
RESUMEN
Se calcula la masa física del mesón escalar s utilizando su función espectral. La función espectral es calculada considerando que la partícula sigma se acopla a un par de piones virtuales π+-π-. El propagador de σ es evaluado después de calcular la autoenergía, cuya parte real es dada por una integral divergente que requiere ser regularizada. Al realizar la regularización mediante el proceso de una substracción simple en la relación de dispersión, se obtiene una expresión analítica cerrada para la parte real de la autoenergía, lo que permite evaluar la función espectral en una forma cerrada. Definiendo la masa física del mesón como la magnitud del cuadrimomentum |k| para la cual la función espectral S(k) obtiene su máximo valor, se obtiene elvalor de 600 MeV para la masa del σ. Este valor es consistentecon el valor experimental reportado en las tablas para la masa de esta partícula. Adicionalmente, también se obtiene que el ancho de esta resonancia tiene un valor alrededor de 220 MeV. Un reporte muy reciente establece el valor de 441 MeV para la masa del sigma. Tomando este valor para ms, obtenemos en nuestros cálculos que la masa física es de 400 MeV.
Palabras clave: mesón sigma, mesones escalares, mesones ligeros.
ABSTRACT
The present research calculates the physical mass of the sigma scalar meson using the spectral function. The spectral function was obtained considering the sigma particle couples with a pair of virtual pions. Sigma ́s propagator was then evaluated, which its real part is a result of a divergent integral, which requires to be regularized. Afterwards, with a simple substraction, a closed analytical expression of the real part of the autoenergy is obtained, which then is used to evaluate the closed form of the spectral function. Defining the meson ́s physical massas the magnitude of the cuadrimomentum in which the spectral function has its maximum value, the mass of thesigma meson is obtained, which is 600 MeV. This value agrees with the experimental values reported in literature. Additionally, the width of the resonance was calculated, as 220 MeV. Recent studies established the sigma meson ́s mass as of 441 MeV, using this information in our method a physical mass of 400 MeV was obtained.
Keywords: sigma meson, scalar mesons, light mesons, spectral function.
El interés por estudiar las propiedades de los hadrones tanto en el vacío como en el medio nuclear se ha incrementado notablemente durante las últimas dos décadas debido a los importantes desarrollos tecnológicos en el campo de los aceleradores y detectores de partículas. La posibilidad de reproducir en el laboratorio las condiciones que se presentaron en el universo en los primeros microsegundos después del Big Bang ha generado una intensa actividad científica en este campo (CERN, s.a; Jacak y Muller, 2012; Fodor, 2012; Morita et al., 2000).
El estudio de las partículas que interaccionan mediante la fuerza fuerte se realiza mediante la cromodinámica cuántica (CDC). Esta teoría ha sido muy exitosa para explicar los fenómenos a elevadas energías, sin embargo, presenta grandes dificultades para resolver sus ecuaciones a bajas energías. La CDC es una de de las teorías fundamentales de la física, siendo sus grados de libertad los quarks y los gluones. Se espera que con ella se puedan describir los procesos de las partículas que interaccionan mediante la fuerza fuerte. No obstante, cuando se estudian los hadrones, que son partículas formadas por quarks, la CDC sevuelve inmanejable (Bowmana et al., 2004).
La cromodinámica cuántica predice la liberación de los quarks a elevadas temperaturas o altas densidades de la materia. En estos procesos de colisiones ultrarrelativistas entre iones pesados que actualmente se llevan a cabo en laboratorios como el European Organization for Nuclear Research (CERN, por sus siglas en francés) o el Relativistic Heavy Ion Collider (RHIC) enEstados Unidos. En el RHIC se reportó, en 2005, la observaciónde un nuevo estado de la materia: el plasma de quarks y gluones(PQG) (Pasechnik y Sumbera, 2017).
Para estudiar las propiedades físicas de este nuevo estado de la materia, es importante comprender el comportamiento del mesón σ en la materia nuclear. Es por eso que la partícula escalar sigma juega un papel importante en esta búsqueda de la transición de fase de la materia nuclear al PQG. Éste es uno de los motivos por los cuales su estudio ha atraído la atención de investigadores de todo el mundo (Ayala et al., 2009; Albaladejo y Oller, 2012).
El estudio del mesón escalar sigma es interesante debido a su carácter controversial. Algunos suponen que es una resonancia de dos piones, es decir, que es generada por la interacción y fusión de dos piones. Otros grupos de investigadores aseguran que los dos piones dentro de la partícula sigma han perdido su identidad, resultando en una estructura de cuatro quarks (Kenkyu, 2001; Close y Tornqvist, 2002).
Un gran número de trabajos se han publicado para calcular la masa y el ancho del mesón escalar sigma tanto en el vacío como en la materia nuclear sometida a condiciones extremas deelevada densidad (Albaladejo y Oller, 2012; Parganlija y Giacosa, 2017). La importancia de este estudio radica en que nos ayudaa comprender y analizar los resultados de los experimentos de choques entre iones pesados ultrarrelativistas. Estos experimentos se están realizando actualmente en el CERN y en el Large Hadron Collider (LHC) (CERN, s.a; Jacak y Muller, 2012).
En este trabajo hemos calculado la masa y el ancho del mesón escalar sigma en el vacío usando la lagrangiana de interacción introducida en Wolf, Friman y Soyeur (1998). Una extensión de este trabajo sería el cálculo de estas cantidades físicas en el medio nuclear para tener un estudio comparativo entre ambas condiciones, en el medio nuclear y en el vacío.
LAS PARTÍCULAS ELEMENTALES
Entre las propiedades físicas importantes de una partícula subnuclear inestable se encuentran su masa y su anchura. Definir la masa de una partícula de una manera operativa y que no dé lugar a situaciones ambiguas es una de las preocupaciones de los físicos de partículas elementales. Sin embargo, la forma de definir la masa en la escala de las partículas subnucleares no es única (Shiomi y Hatsuda, 1994; Kim et al., 1999; Jean, Piekarewicz y Williams, 1994; Dutt-Mazumder, Kundu y De, 1996).
El concepto de función espectral (Asakawa et al., 1992; Hermann, Friman y Nörenberg, 1993) ha probado ser de gran utilidad para describir el comportamiento de las partículas en el medio nuclear, y la usaremos aquí para calcular la masa del mesón escalar σ en el vacío.
Cuando se estudian las propiedades de una partícula enun medio con el cual interacciona, el problema de definir lamasa de la partícula se vuelve algo complicado. La masa, el momento magnético y otras propiedades de las partículas cambian cuando éstas se encuentran en un medio con el cual interaccionan, volviéndose inclusive difícil definir a la misma partícula en este medio. Una de las técnicas utilizadas para describir una partícula que interacciona con el medio donde se encuentra fue introducida por el físico ruso Lev Landau mediante el concepto de cuasipartícula, el cual engloba a la partícula misma y sus interacciones. Tenemos entonces que la cuasipartícula se vuelve algo difusa, con atributos que dependen de las interacciones que queramos incluir en sudefinición y también del modelo utilizado para definirla (Mattuck, 1992).
La existencia misma de la partícula sigma estuvo sujeta a muchas controversias, sin embargo, debido a su importancia en modelos teóricos que han sido exitosos, esta partícula ha sido objeto de intenso estudio teórico. El Modelo Sigma Lineal y el Modelo de Nambu and Jona-Lasinio son ejemplos de la importancia del sigma en el estudio de la dinámica de hadrones (Kunihiro, 1995). Tanto sus propiedades en el vacío como en la materia nuclear y su estructura misma han atraído la atención de los investigadores teóricos. Actualmente, su existencia experimental ha sido probada al ser observada en los procesos de dispersión entre dos protones PP→PP. El anuncio de la detección de la partícula sigma fue realizado en un artículo en 2001 (Aitala et al., 2001) y actualmente aparece en la publicación Particle Data Group (PDG) (Patrignani et al., 2017) como una resonancia de dos piones con una masa de 500 MeV también llamada ?(500).
La determinación de las masas de las partículas es, por supuesto, fundamental para entender la naturaleza a escalas subatómicas. Por otra parte, para comprender los fenómenos a escala de estrellas, galaxias y cosmológicos es importante conocer las propiedades de las partículas subatómicas. Este maridaje entre lo más pequeño y lo más grande ha originado nuevos campos de la física como la astrofísica nuclear. Debido a estos fenómenos que relacionan los fenómenos a escalas cosmológicas y subatómicas, la física de partículas y la cosmología se estudian ahora en forma combinada.
Propagadores
En este trabajo se realizan cálculos para determinar la masa física del mesón escalar sigma suponiendo que es una resonancia de dos piones y que, por tal motivo, al interaccionar con el vacío cuántico, el mesón σ pue-de acoplarse a dos piones virtuales ?+-?-. Se utilizan las técnicas de la teoría cuántica relativista de campos para calcular el propagador de la partícula, y de éste se calculala masa física del sigma. La masa así obtenida, se espera que corresponda, dentro de los límites de precisión de los experimentos, a la masa observada experimentalmente.
El concepto de propagador es fundamental en la teoría cuántica de campos y en este trabajo se emplea extensivamente. El propagador de una partícula, como su nombre lo indica, describe la propagación de ésta en el medio que estamos considerando. El propagador es una expresión matemática que describe la evolución temporal o la propagación en el tiempo y en el espacio de la partícula. En general, el propagador está dado por una expresión de variable compleja, la cual tiene una parte real y otra imaginaria. Una de las convenciones para definir la masa de una partícula es a través del propagador en el espacio de momentos D(k), estableciendo que ésta está dada por la posición del polo del propagador D(k).Otra forma de definir la masa de la partícula es utilizando la función espectral S(k), la cual es definida como -2? veces la parte imaginaria del propagador. En este caso la masa de la partícula corresponde al valor absoluto |k| del momentum de la partícula, donde S(k) obtiene su máximo.
Propagador para el campo escalar
Desde inicios del siglo XX, cuando Einstein explicó el efecto fotoeléctrico introduciendo el concepto de fotón, lo que implica un comportamiento corpuscular de la luz, la descripción dual, de onda y partícula para los campos y las partículas a la escala atómica, es la que determina correctamente su comportamiento físico. La teoría moderna que describe el comportamiento de las partículas subatómicas es la teoría cuántica de campos. En esta teoría las partículas se comportan como campos, y viceversa. En el campo electromagnético, el más estudiado y el mejor conocido de los campos, la luz es considerada en algunos experimentos como la propagación de una onda electromagnética, es decir, como un campo electromagnético que depende del tiempo y el espacio, propagándose aun en el vacío. Por otra parte, en ciertos fenómenos, la luz exhibe un comportamiento de partícula, a esta partícula se le conoce como fotón. La teoría cuántica del campo electromagnético es el estudio del fotón en interacción con las partículas cargadas.
El campo más sencillo en la teoría cuántica de campos es el escalar, el cual representa partículas sin espín. El propagador asociado con este campo para una partícula libre se conoce como propagador libre, escrito como ∆º(k). En el espacio de momentos su forma analítica está dada por:
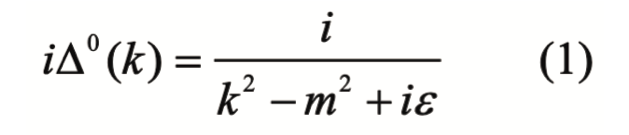
Donde k es el momento de la partícula y m la masa desnuda de la partícula, la cual corresponde a la masa del campo cuando no hay interacciones. Como se aprecia de la ecuación (9), la masa desnuda corresponde al valor positivo de k donde ?∆º (k) tiene un polo (Lurié, 1968).
Al tomar en consideración las interacciones de la partícula, su propagación se ve afectada, manifestándose este efecto en un cambio en la expresión matemática del propagador. Al propagador que describe la partícula con sus interacciones se le llama propagador modificado o vestido (Serot y Walecka, 1986).
Esquemáticamente, los propagadores modificados a primer orden, segundo orden, etc., hasta el propagador completo, ∆¹(k), ∆²(k) , …, ∆(k), respectivamente, se representan en teoría de perturbaciones mediante diagrama de lazos y líneas.
Analíticamente el propagador completo ∆(k), que se expresa como una suma infinita:
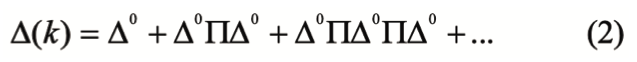
donde Π representa las interacciones de la partícula en su propagación y es llamada autoenergía de la partícula.
Esta expresión puede escribirse de la siguiente manera:

La ecuación (3) es conocida como la Ecuación de Dyson, de donde se obtiene que:
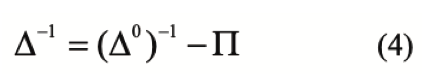
La solución para el propagador modificado ∆(k) está dada por:
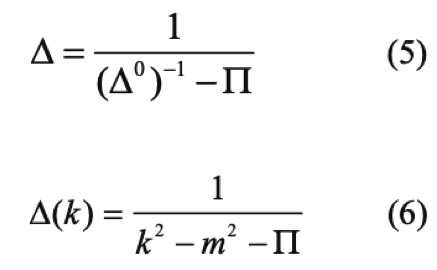
Observamos que, de acuerdo con nuestra definición de masa de la partícula (definida como el polo del propagador), ésta ha cambiado debido a la interacción, la cual hemos designado con Π (autoenergía).
Uno de nuestros objetivos es determinar la interacción de la partícula, la cual aparece en la función de autoenergía Π(k).
Marco teórico
La importancia de los mesones ligeros en problemas de física nuclear, materia nuclear sometida a condiciones extremas depresión y temperatura, astrofísica y cosmología, se ha puesto de manifiesto recientemente en el estudio de colisiones de núcleos pesados a energías ultrarrelativistas. La determinaciónde las propiedades físicas de los mesones se ha convertido en un asunto de gran importancia para la física de partículas.
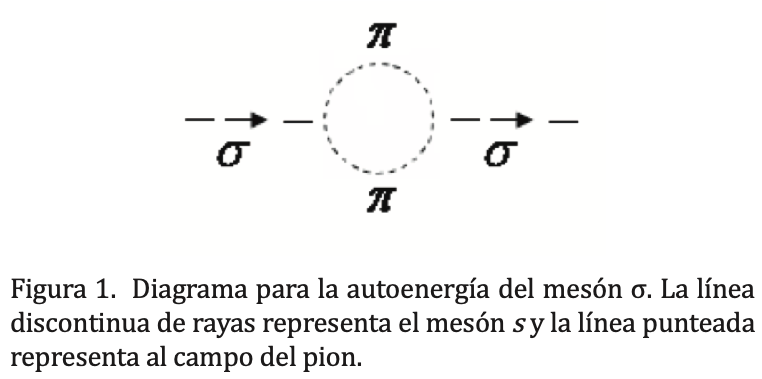
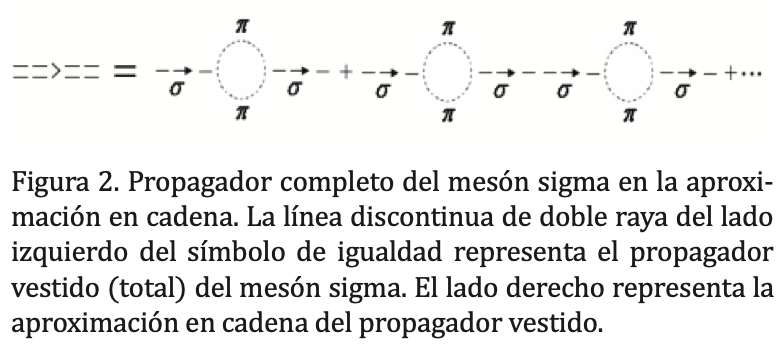
La influencia de la interacción del mesón σ con un par de piones virtuales es introducida a través de la modificación del propagador libre en la aproximación de un solo lazo. Ésta se muestra gráficamente en la figura 1. La contribución de este diagrama de Feynman introduce la autoenergía del mesón sigma. Se calcula el propagador completo en la aproximación encadena (Chin, 1977), la cual consiste en una suma infinita detérminos de autoenergía de un solo lazo de la forma mostrada en la figura 1. La representación diagramática se muestra en la figura 2, mientras que la expresión analítica está dada por ?∆(k) cuyo resultado aparece en la ecuación (7).
La lagrangiana de interacción entre el mesón sigma y los dos piones está dada por

La solución de la ecuación de Dyson para el propagador vestido está dada por
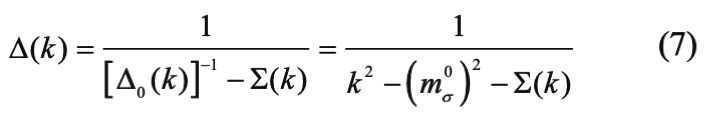
Por otra parte, la expresión analítica para la autoenergía ?(k), está dada por (Jean, Piekarewicz y Williams, 1994; Asakawa et al., 1992):
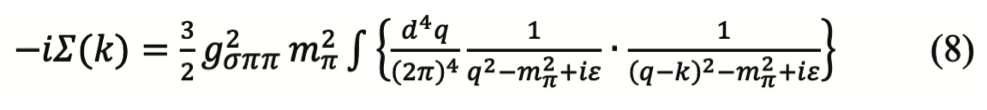
Donde el coeficiente 3/2 para el lazo del pion proviene de los tres estados de isospín y del factor de la simetría por permutación (Wolf, Friman y Soyeur, 1998).
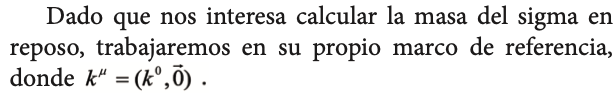
RESULTADOS

y para la función espectral S(k), partiendo de la definición dada anteriormente, como -2? veces la parte imaginaria del propagador, toma la forma
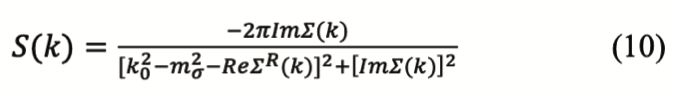
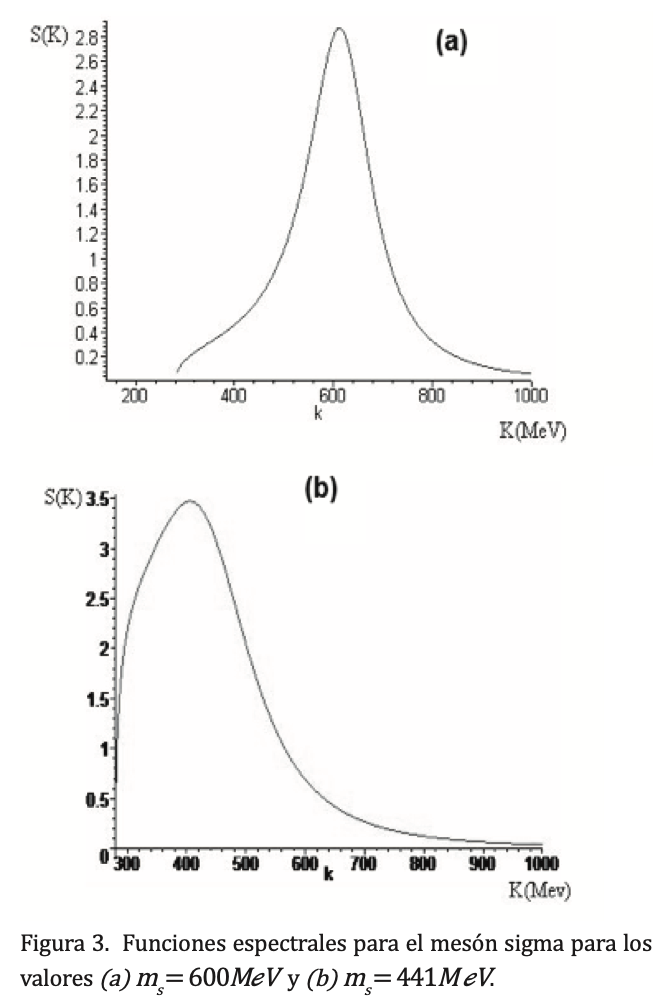
Sustituyendo los valores obtenidos para Im?(k²) y Re?ᴿ(k²) en la ecuación (10) obtenemos una expresión cerrada para la función espectral. Los parámetros que aparecen en la ecuación (10) son los valores reportados para la masa m? del mesón σ, el cual toma el valor de 660 MeV. Recientemente ha sido reportado el valor experimental de 441 MeV para la masa del sigma. Para ambos casos, las gráficas de S(k) obtenidas de la ecuación (10) se muestran en las partes a) y b) de la figura 3, tomando para la constante de acoplamiento entre el mesón sigma y los dos piones el valor gσππ=12.8 (Wolf, Friman y Soyeur, 1998).
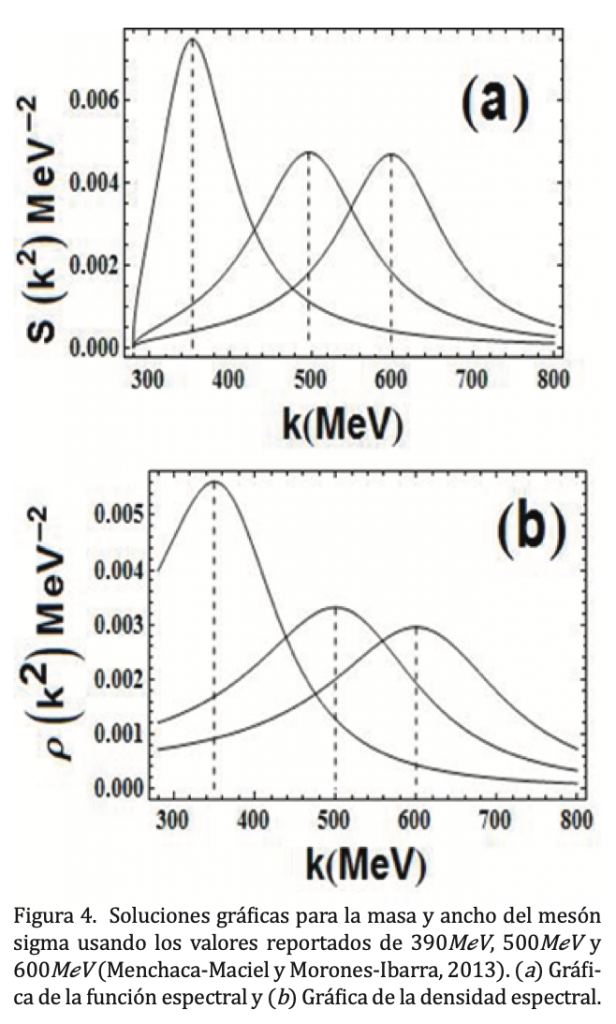
Los resultados finales se obtienen de las gráficas de la función espectral mostradas en la figura 3. Ahí se observa, en la gráfica a), que para ms =600 MeV el pico de S(k)corresponde también a 600 MeV, resultado que está en concordancia con los que aparecen en las tablas para la masa del mesón sigma (Saito et al., 1998). Dado que en un artículo reciente (Leutwyler, 2007) se estimó la masa del mesón Sigma en 441 MeV, se incluye también este caso en la gráfica b) de la figura 3. El valor de la masa para este caso es de 400 MeV.
CONCLUSIONES
En el análisis teórico de la propagación del mesón σ en el vacío hemos calculado su masa física, obteniendo un resultadoque está en perfecto acuerdo con el reportado en el (PDG) para ?(500) (Kunihiro, 1995). Se observa que el valor de la masa física, determinada por el pico de la función espectral, es bastante sensible al valor de la masa inicial seleccionada, en concordancia con los resultados esperados. El uso de una sustracción simple en la relación de dispersión ha permitido regularizar la expresión para la parte real de la autoenergía ReS (k²), dando una expresión analítica cerrada. El principal resultado de este trabajo es que hayamos podido obtener la masa física del mesón s , bajo la consideración de que éste se acopla en el vacío a dos piones virtuales cargados. Este resultado representa una fuerte evidencia de que el mesón s puede considerarse como una resonancia de dos piones.
* Universidad Autónoma de Nuevo León.
Contacto: rubenmorones@yahoo.com.mx
REFERENCIAS
Aitala, E.M., et al. (2001). Experimental Evidence for a Light and Broad Scalar Resonance in D+→π−π+π+ Decay. Phys. Rev. Lett. 86, 770.
Albaladejo, M., y Oller, J.A. (2012). Size of the σ meson andits nature. Phys. Rev. D 86 034003.
Asakawa, M., Ko, C.M., Lévai, P., et al. (1992). Rho meson indense hadronic matter. Phys. Rev. C 46 R1159.
Ayala, A., Bashir, A., Raya, A., et al. (2009). Chiral phasetransition in relativistic heavy-ion collisions with weakmagnetic fields: Ring diagrams in the linear sigma model. Phys. Rev. D 80.
Bowmana, P.O., Hellerb, U.M., Leinwebera, D.B., et al.(2004). Infrared and ultraviolet properties of the Landaugauge quark propagator. Nuclear Physics. B(Proc.Suppl.). 128: 23-29.
CERN. (s.a). Heavy ions and quark-gluon plasma. Disponible en http://home.web.cern.ch/about/physics/heavy-ions-and-quark-gluon-plasma
Chin, S.A. (1977). A relativistic many-body theory of highdensity matter. Ann. Phys. 108(2): 301-367.
Close, F.E., y Tornqvist, N.A. (2002). Scalar mesons above and below 1 GeV. J. Phys. G 28 R249.
Dutt-Mazumder, A.K., Kundu, B.D.R.A., y De, T. (1996). Tensor coupling and vector mesons in dense nuclear matter. Phys. Rev. C 53 790.
Fodor, Z. (2012). Selected results in lattice quantum chro-modynamics PTEP2012 01A108. Prog. Theor. Exp. Phys.
Hermann, M., Friman, B., y Nörenberg, W. (1993). Properties of ρ-mesons in nuclear matter. Nucl. Phys. A560 411.
Jacak, B.V., y Muller, B. (2012). The exploration of hot nuclear matter. Science. 337- 310.
Jean, H.C., Piekarewicz, J., y Williams, A.G. (1994). Medium modifications to the ω-meson mass in the Walecka model. Phys. Rev. C 34.
Kenkyu, S. (kyoto). (2001). Possible existence of the sigma-meson and its implications to hadron Physics. KEK Proceedings 2000-4. 102 E1. The proceedings of this workshop.
Kim, Y., Rapp, R., Brown, G.E., et al. (1999). A schematic model for density dependent vector meson masses. RHIC Physics and Beyond. 17 (American Institute of Physics, CP482).
Kunihiro, T. (1995). A Geometrical Formulation of the Renormalization Group Method for Global Analysis. Progress of Theoretical Physics. 94(4): 503-514.
Leutwyler,H.(2007).Mass and Width of the σ. Int. J. Mod. Phys., A 22(2-3): 257-265.
Lurié, D. (1968). Particles and Fields. EE.UU.: Interscience Publishers, p 266.
Mattuck, R.D. (1992). A Guide to Feynman Diagrams in the Many Body Problem. EE.UU. Dover Publications Inc.
Menchaca-Maciel, M.C., y Morones-Ibarra, J.R. (2013). Sigma meson in vacuum and nuclear matter. J.R., Indian J. Phys. 87(4): 385-390.
Morita, K., Muroya, S., Nakamura, H., et al. (2000). Numerical analysis of a two-pion correlation function based on a hydrodynamical model. Phys. Rev. C 61, 034904.
Parganlija, D., y Giacosa, F. (2017). The ƒ₀ (1790) and ?₀ (1950) Resonances as Excited qq Statesin the Extended Linear Sigma Model. Eur. Phys. J. C.77(7): 450.
Pasechnik, R., y Sumbera, M. (2017). Phenomenological
Review on Quark–Gluon Plasma: Concepts vs. Observations. Universe. 3(1): 7.
Patrignani, C., Agashe, K., Aielli, G., et al. (2017). Review ofparticle physics. Chinese Physics. C 40(10).
Saito, K., Tsushima, K., Thomas, A., et al. (1998). σ and ω meson propagation in a dense nuclear medium. Phys. Lett. B. 433(3-4): 243-249.
Serot, B.D., y Walecka, J.D. (1986). The Relativistic Nuclear Many Body Problem. Adv. Nucl. Phys. 16:1-327.
Shiomi, H., y Hatsuda, T., (1994). Vector mesons in nuclearmedium-an effective lagrangian approach. Phys. Lett. B. 334 281.
Wolf, G., Friman, B., y Soyeur, M. (1998b). In-medium ω-meson broadening and s-wave pion annihilation into e+e− pairs. Nucl. Phys. A. 640(1): 129-143.
RECIBIDO: 28/01/2018
ACEPTADO: 23/04/2018
