Una metaheurística con reencadenamiento de trayectorias para optimizar planes territoriales
*Roger Z. Ríos Mercado*, Hugo Jair Escalante Balderas**
CIENCIA UANL / AÑO 21, No. 87 enero-febrero 2018
RESUMEN
Dado un conjunto de unidades geográficas con información conocida de número de clientes, demanda de producto, carga de trabajo y localización espacial, el problema bajo estudio consiste en encontrar una división o partición de las mismas en conjuntos (denominados territorios o distritos) que minimicen una medida de dispersión territorial y que cumplan con requerimientos importantes como conectividad territorial y balance territorial con respecto al número de clientes, demanda de producto y carga de trabajo. El presente trabajo propone una metodología heurística para la solución de este problema, la cual integra varios componentes, como un método voraz-adaptativo, una búsqueda local y un componente de mejora basado en reencadenamiento de trayectorias. Todos estos componentes explotan inteligentemente la estructura matemática del problema. La evidencia empírica sobre un conjunto de instancias de prueba revela el impacto positivo de cada uno de los componentes desarrollados en términos de calidad de la solución y tiempo de ejecución.
Palabras clave: investigación de operaciones, optimización combinatoria, diseño de territorios comerciales, localización discreta; metaheurísticas.4.
ABSTRACT
Given a set of geographical units with the information known from a number of clientes, product requests, workload and spatial location; the probleme of this study consist in finding a division or partition from the same ground in assemblies (called districts or areas) that minimize a measure of territorial dispersion to fulfill with the important requirements such as territorial conectivity and territorial balance with respect to the number of clients, product requests and workload. This current work proposes a heuristic metodology to fix this problem which involve several components, as an adaptive selection method, a local research and an upgrade component based on relinking trajectories. All of these componentes intelligently exploit the problem’s mathematical structure. The empiric evidence about an assembly of probationary request reveals a positive impact of each of the components developed in terms of quality of the solution and execution time.
Keywords: Operations research, combinatorial optimization, comercial area designs, discreet location; heuristics.
El problema de diseño territorial (TDP por sus siglas en inglés, Territory Design Problem) puede definirse como el problema de agrupar pequeñas unidades básicas geográficas (BUs) en grupos más grandes denominados territorios o distritos, de tal forma que éstos son aceptables (u óptimos) de acuerdo a ciertos criterios de planificación (Kalcsics, Nickel y Schröder, 2005). El campo de diseño territorial o distriteo tiene un amplio rango de aplicaciones, como el diseño de distritos electorales, diseño de territorios de ventas, diseño de distritos escolares, diseño de distritos para servicios públicos y diseño de territorios comerciales, por nombrar los más relevantes.
El problema estudiado en este trabajo es un problema de diseño de territorios comerciales (CTDP, por sus siglas en inglés) motivado por una aplicación real proveniente de la industria de bebidas embotelladas. El problema, introducido por Ríos-Mercado y Fernández (2009), consiste en encontrar un diseño de p territorios de mínima dispersión sujeto a requerimientos de planificación como conectividad territorial, asignación única de BUs a territorios y balance territorial con respecto a tres atributos asociados con las BUs: número de puntos de venta, demanda del producto y carga de trabajo. Brevemente, el requerimiento de conectividad territorial implica que en cada territorio las BUs deben estar conectadas de tal forma que exista una ruta entre ellas contenida totalmente en el territorio. El requerimiento de asignación única de BUs a territorios implica que cada BU debe ser asignada única y exclusivamente a un solo territorio, garantizando una partición correcta. El requerimiento de balance territorial significa que cada territorio debe tener, en su totalidad, un valor muy parecido del atributo medible en cada BU.
Un criterio de marcada importancia en TDPs es la compacidad territorial. Típicamente, esto se logra mediante la minimización de una función métrica de dispersión territorial. Se han estudiado algunos modelos basados en funciones de dispersión provenientes de los conocidos modelos de localización de p-centro (Elizondo-Amaya, Ríos-Mercado y Díaz, 2014; Ríos-Mercado y Fernández, 2009; Salazar-Aguilar, Ríos-Mercado y Cabrera-Ríos, 2011) y p-mediana (Ríos-Mercado y López-Pérez, 2013; Salazar-Aguilar, Ríos-Mercado y Cabrera-Ríos, 2011; Salazar-Aguilar et al., 2012). Estas funciones de dispersión están basadas en centros territoriales, es decir, la dispersión se mide con distancias euclídeas de las BUs al centro o centroide de su territorio. Este tipo de funciones basadas en centroides dependen fuertemente de la ubicación de los mismos. Si los centroides no están ubicados apropiadamente, el diseño territorial resultante puede causar un serio deterioro en la función objetivo. Además, en problemas de localización, los centroides representan un ente o instalación física que provee algún tipo de servicio; sin embargo, en CDTP, los centroides se ubican artificalmente, ya que en realidad no existe ningun servidor que se ubique en dicho centroide, es simplemente un recurso para tener un punto de referencia y poder calcular la medida de dispersión.
Estas limitaciones de los modelos existentes motivan a estudiar otro tipo de métricas de dispersión territorial. Por ejemplo, una medida es el diámetro que mide la distancia más grande entre dos BUs en un territorio. Esta métrica es una función más robusta, ya que no depende de la ubicación de ningún centroide, proveyendo una mayor flexibilidad. Inclusive, otra gran ventaja puede verse desde la perspectiva del desarrollo de algoritmos de solución. Los métodos heurísticos para intentar resolver TDPs bajo funciones de dispersión basadas en centroides tienen que llevar a cabo constantemente procedimientos de actualización y recálculo de centroides, ya que éstos se mueven cada vez que un territorio sufre un cambio. Estas tareas de actualización y recálculo, bastante pesadas computacionalmente hablando, pueden evitarse si se usan otras métricas no basadas en centroides como el diámetro, por ejemplo. En este trabajo de investigación nos enfocamos en el estudio de un problema de diseño territorial comercial que busca minimzar la dispersión territorial basado en una función tipo diámetro, totalmente independiente de los centroides territoriales. Hasta donde tenemos cono- cimiento, este problema, tal cual, no ha sido estudiado en la bibliografía.
Como la meta es poder resolver instancias de gran escala, se propone e implementa un método de solución metaheurística conformado por un procedimiento de búsqueda ávida aleatoria adapativa (GRASP, por sus siglas en inglés, Greedy Randomized Adaptive Search Procedure) con reencadenamiento de trayectorias (PR, por sus siglas en inglés, Path Relinking). Denotamos a nuestro algoritmo como GPR-CTDP. En el componente constructivo de GRASP, hemos propuesto y desarrollado un procedimiento que construye exactamente p territorios de forma simultánea, es decir, el algoritmo empieza sembrando temporalmente p nodos (BUs) como semillas y posteriormente, de forma iterativa, va asignando el resto de las BUs a estas semillas hasta que todas las BUs han sido asignadas. Además, se han propuesto y desarrollado dos estrategias de reencadenamiento de trayectorias: una estática y otra dinámica, motivados por el trabajo de Resende et al. (2010).
En nuestro trabajo de investigación, estas estrategias de PR dependen de encontrar una “ruta” entre dos diferentes soluciones de diseño territorial. Para este propósito se plantea y resuelve un subproblema de asignación asociado para encontrar el mejor aparea- miento entre los centroides territoriales de ambos diseños. La solución a este subproblema provee una manera bastante elegante y eficiente de generar la trayectoria entre estos dos diseños dados. Esta idea es novel en la bibliografía de diseño territorial, convirtiéndose en otra contribución científica importante del trabajo.
Para evaluar la eficiencia del algoritmo propuesto, cada uno de sus componentes y estrategias son extensivamente probados en una amplia base de datos de instancias del problema, lo cual demuestra la gran calidad y aporte de cada uno de los componentes, lo cual resulta en un algoritmo bastante potente, eficiente y robusto que aporta soluciones a instancias bastante grandes del problema en tiempos de cómputo razonablemente pequeños.
DESCRIPCIÓN DEL PROBLEMA
Sea G = (V, E) un grafo donde V es el conjunto de manzanas o unidades básicas (BUs) y E es el conjunto de aristas representando adyacencia entre manzanas, es decir (i, j) e E si y sólo si BUs i y j son manzanas adyacentes. Sea ![]() la distancia euclídea entre BUs i y j, con i, j ∈ V. Para cada BU i∈V hay tres parámetros o atributos asociados. Sea
la distancia euclídea entre BUs i y j, con i, j ∈ V. Para cada BU i∈V hay tres parámetros o atributos asociados. Sea ![]() el valor del atributo a en el nodo i, donde a = 1, 2 y 3, representa el número de clientes, demanda de producto y carga de trabajo, respectivamente. El número de territorios es conocido y dado por el parámetro p. Una p-partición de V se denota por X=(X1,…,Xp) , donde Xκ ⊂ V es un territorio de V. Sea wª (Xκ )=
el valor del atributo a en el nodo i, donde a = 1, 2 y 3, representa el número de clientes, demanda de producto y carga de trabajo, respectivamente. El número de territorios es conocido y dado por el parámetro p. Una p-partición de V se denota por X=(X1,…,Xp) , donde Xκ ⊂ V es un territorio de V. Sea wª (Xκ )= ![]() el tamaño del territorio
el tamaño del territorio ![]() con respecto a la actividad a ∈ A = {1, 2, 3}y k ∈ K = {1,…,p}. Las restricciones de balance territorial se modelan mediante la introducción de un parámetro de tolerancia ta aque mide la desviación relativa permitida de una meta promedio μª , dada por μª =wª (V)/ p , para cada a∈ A. Otro requerimiento es que todos los nodos asignados a un territorio están conectados por una ruta contenida totalmente en el territorio. Finalmente, se persigue minimizar la dispersión territorial. Sea Π la colección de todas las p-particiones de V. El modelo de optimización combinatoria (CTDP) está dado por:
con respecto a la actividad a ∈ A = {1, 2, 3}y k ∈ K = {1,…,p}. Las restricciones de balance territorial se modelan mediante la introducción de un parámetro de tolerancia ta aque mide la desviación relativa permitida de una meta promedio μª , dada por μª =wª (V)/ p , para cada a∈ A. Otro requerimiento es que todos los nodos asignados a un territorio están conectados por una ruta contenida totalmente en el territorio. Finalmente, se persigue minimizar la dispersión territorial. Sea Π la colección de todas las p-particiones de V. El modelo de optimización combinatoria (CTDP) está dado por:
El objetivo (1) mide la dispersión territorial. Las restricciones (2) representan el balance territorial con respecto a cada atributo. Las restricciones (3) garantizan la conectividad territorial, donde Gκ es el grafo inducido en G por el conjunto de nodos ![]() . Nótese que hay un número exponencial de estas restricciones. El CTDP es NP-duro (Ríos-Mercado y Fernández, 2009).
. Nótese que hay un número exponencial de estas restricciones. El CTDP es NP-duro (Ríos-Mercado y Fernández, 2009).
DESCRIPCIÓN DE LA HEURÍSTICA
Como se indicó en la sección anterior, todos los métodos existentes desarrollados para la distribución comercial no son aplicables en este caso, dada la naturaleza de la función objetivo que se optimiza. Es necesario desarrollar software específico.
En esta sección se presenta GPR-CTDP, una heurística GRASP con reencadenamiento de trayectorias para el problema en cuestión. GRASP es una metaheurística bien conocida basada en mecanismos de búsqueda ávida y construcción aleatorizada (Feo y Resende, 1995) que se ha utilizado con éxito para muchos problemas de optimización combinatoria, incluyendo CTDP (Ríos-Mercado y Fernández, 2009). Proponemos un GRASP mejorado con reencaminamiento de trayectorias. Naturalmente, se espera que la incorporación de un mecanismo de búsqueda sofisticado como PR proporcione soluciones de mucho mejor calidad que las obtenidas mediante la simple búsqueda local. La heurística comprende un nuevo procedimiento de construcción y un mecanismo de PR muy eficaz. El procedimiento de construcción maneja inteligentemente una estrategia para construir territorios simultáneamente, mientras que el PR nos permite obtener soluciones de mucho mejor calidad que las obtenidas con la búsqueda local simple. El detalle de los componentes de la heurística pueden encontrarse en Ríos-Mercado y Escalante (2016).
Reencadenamiento de trayectorias
El reencadenamiento de trayectorias fue originalmente propuesto por Glover y sus colegas como una forma de incorporar estrategias de intensificación y diversificación en la búsqueda tabú (Glover, 1996). PR consiste en explorar la trayectoria de las soluciones intermedias entre dos soluciones seleccionadas llamadas ![]() y
y ![]() con la hipótesis de que algunas de las soluciones intermedias pueden ser mejores que
con la hipótesis de que algunas de las soluciones intermedias pueden ser mejores que ![]() y
y ![]() (intensificación) o comparables, pero suficientemente diferentes de
(intensificación) o comparables, pero suficientemente diferentes de ![]() y
y ![]() (diversificación). Las soluciones intermedias se generan realizando movimientos desde la solución inicial
(diversificación). Las soluciones intermedias se generan realizando movimientos desde la solución inicial ![]() hasta la solución guía
hasta la solución guía ![]() , de tal manera que estos movimientos introducen atributos que están presentes en la solución guía
, de tal manera que estos movimientos introducen atributos que están presentes en la solución guía ![]() .
.
En el contexto de GRASP, PR puede ser considerado como una forma de introducir la memoria en el proceso de búsqueda. Hasta donde sabemos, el PR no se ha utilizado en el contexto del diseño de territorios. En este trabajo se consideran dos variantes de PR hacia adelante-y-hacia atrás, llamadas estática y dinámica, que han demostrado ser muy efectivas en problemas relacionados (Resende et al., 2010).
Las denominadas estrategias de PR hacia adelante-y-hacia atrás exploran las rutas entre ![]() y
y ![]() de dos maneras diferentes (es decir, de
de dos maneras diferentes (es decir, de ![]() y
y ![]() y viceversa). El principal beneficio de estas estrategias es que se pueden generar más y diferentes soluciones, aunque se ha encontrado que hay poca ganancia sobre las estrategias unidireccionales (Ribeiro, Uchoa y Werneck, 2002).
y viceversa). El principal beneficio de estas estrategias es que se pueden generar más y diferentes soluciones, aunque se ha encontrado que hay poca ganancia sobre las estrategias unidireccionales (Ribeiro, Uchoa y Werneck, 2002).
Esto puede deberse a la codicia de los métodos de PR habituales, los cuales evaluán todas las posibles soluciones que se pueden generar al hacer un movimiento desde una solución inicial y elegir el movimiento que da como resultado la mejor solución intermedia. Por lo tanto, estos métodos exploran un gran número de soluciones y, por ende, el PR hacia adelante no ayuda a mejorar la calidad de las soluciones. En este trabajo seleccionamos movimientos de tal manera que se evalúa un solo movimiento para generar soluciones intermedias. Esta forma de PR es más eficiente a expensas de sacrificar un poco el beneficio de estrategias ávidas. Los detalles de la implementación pueden encontrarse en Ríos-Mercado y Escalante (2016).
RESULTADOS COMPUTACIONALES
En esta sección se presentan los resultados experimentales obtenidos con GPR-CTDP. El método propuesto fue implementado en MATLAB®. Todos los experimentos se ejecutaron en una estación de trabajo de 64 bits con un procesador Corei7 a 3.4 GHz y 8 GB en RAM. Para los experimentos utilizamos la base de datos de Ríos-Mercado y Fernández (2009). Se trata de instancias generadas aleatoriamente basadas en datos de instancias reales. Los conjuntos de datos DS y DT se consideran para la experimentación. El primer conjunto genera los pesos de las BUs a partir de una distribución uniforme y el segundo utiliza una distribución triangular. Estos conjuntos de datos se describen completamente en Ríos-Mercado y Fernández (2009). Para cada uno de los conjuntos de datos DS y DT hay 20 instancias diferentes de tamaño n = 500 y p = 10. Para todas las instancias de los conjuntos de datos usamos un nivel τª = 0.05, a ∈ Α. A lo largo de la evaluación, el GRASP se ejecuta con i max= 500. Basado en la experimentación preliminar para calibrar los parámetros algorítmicos de GPR-CTDP, se utilizan los valores reportados en la tabla I.
Evaluación de los procedimientos de construcción y búsqueda local dentro del marco de GRASP
En esta sección se presentan los resultados de los experimentos diseñados para evaluar el efecto de los procedimientos de construcción y búsqueda local. Para ello se aplica la fase de construcción dentro de un marco GRASP, es decir, no se aplica ninguna fase PR en este experimento. Primero aplicamos el GRASP sólo con fase de construcción y luego aplicamos el GRASP completo con fases de construcción y búsqueda local (no PR). Para cada ejecución probamos los dos conjuntos de datos DT y DS.
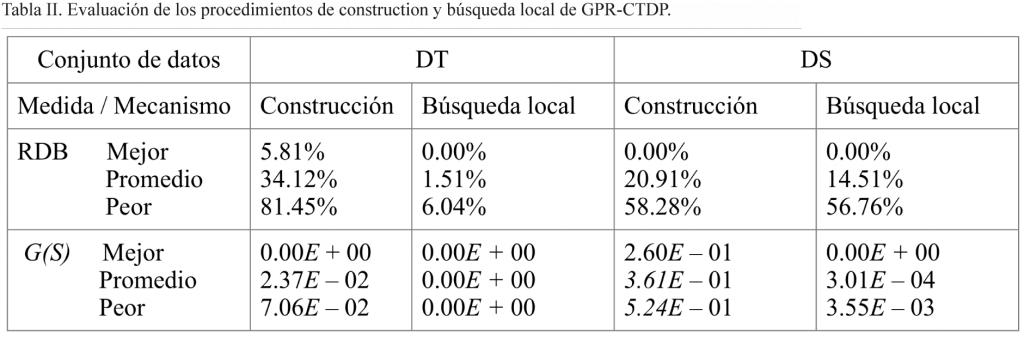
La tabla II resume el desempeño de los procedimientos de construcción y búsqueda local en todas las instancias de los conjuntos de datos DT y DS. Para el término de dispersión (función objetivo) F(S), se muestra la desviación relativa entre la solución obtenida con cada procedimiento y la mejor solución conocida para cada instancia, RDB = ![]() La columna etiquetada como “búsqueda local” indica que ambas fases (construcción y búsqueda local) son aplicadas. El término G(S) representa el grado de infactibliad, es decir, mide qué tanto la solución S se desvía de las restricciones de balance. Un valor G(S)=0 significa que no hay violación a las restricciones, es decir, es factible. De esta tabla podemos apreciar que el promedio de la suma de las infactibilidades relativas se mantiene bajo en el procedimiento de construcción para ambos conjuntos de datos. El procedimiento propuesto es capaz de obtener soluciones aceptables en términos del grado de satisfacción de las restricciones de balance a pesar de que parte del procedimiento de construcción se basa en un criterio puramente de distancia.
La columna etiquetada como “búsqueda local” indica que ambas fases (construcción y búsqueda local) son aplicadas. El término G(S) representa el grado de infactibliad, es decir, mide qué tanto la solución S se desvía de las restricciones de balance. Un valor G(S)=0 significa que no hay violación a las restricciones, es decir, es factible. De esta tabla podemos apreciar que el promedio de la suma de las infactibilidades relativas se mantiene bajo en el procedimiento de construcción para ambos conjuntos de datos. El procedimiento propuesto es capaz de obtener soluciones aceptables en términos del grado de satisfacción de las restricciones de balance a pesar de que parte del procedimiento de construcción se basa en un criterio puramente de distancia.
Después de aplicar la búsqueda local a las soluciones construidas, la medida de dispersión F(S) se mejora ya que muestra una reducción importante en la desviación relativa con respecto al mejor valor de dispersión. En el caso del conjunto de datos DT, las soluciones obtenidas con búsqueda local están muy próximas a las mejores en términos de dispersión (desviación media de 1.51%), mientras que para el DS hay mucho más margen de mejora (desviación media de 14.51%). Para el conjunto de datos DT, la función objetivo se mejora en promedio en 32.61%, mientras que para el conjunto de datos DS la mejora es de 6.4%. Éstas son diferencias bastante importantes que evidencían la eficacia del mecanismo de búsqueda local propuesto. Es muy importante destacar que la dispersión se mejora al reducir también considerablemente G(S).
GRASP VS. GPR-CTDP
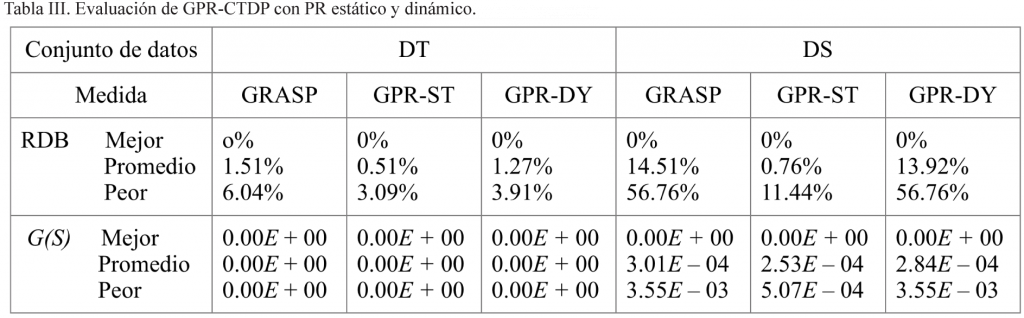
En esta sección se presentan los resultados experimentales de las mejoras de las estrategias de PR sobre la implementación directa de GRASP. La tabla III muestra el rendimiento de GPR-CTDP tanto en la estrategia estática (columnas GPR-ST) como dinámica (columnas GPR-DY) para los conjuntos de datos DT y DS. En la tabla, se compara el rendimiento de GPR-CTDP cuando se utiliza PR y cuando sólo se usa GRASP sin PR. Se muestra la desviación relativa entre la mejor solución obtenida con cada método y la mejor solución conocida para cada caso.
Como podemos ver, para el conjunto DT, las mejoras obtenidas con PR sobre la búsqueda local son relativamente pequeñas mas no despreciables. Creemos que este resultado puede ser debido al hecho de que nos estamos acercando al óptimo global para este conjunto de datos y puesto que el procedimiento de búsqueda local proporciona soluciones muy competitivas por sí mismo, las mejoras debidas a PR son muy pequeñas. Sin embargo, es importante enfatizar que todas las soluciones encontradas con GRASP y GPR-CTDP son factibles para este conjunto de datos. Para DT la estrategia de PR estática superó la dinámica por menos de 1% en términos de la función objetivo. Para el conjunto DS, las mejoras debidas a PR son mayores. De nuevo, GPR-CTDP con PR estático supera los resultados de la búsqueda local en un promedio de cerac de 13% en términos de la función objetivo, mientras que la estrategia dinámica supera la búsqueda local en menos de 1%. La variante estática de PR consigue importantes mejoras en términos del objetivo de dispersión (F(S)), al tiempo que reduce el término de infactibilidad.
CONCLUSIONES
En este trabajo de hemos introducido un nuevo modelo para el CTDP, el cual usa una función de dispersión basada en el diámetro en lugar de las tradicionales métricas basadas en centroides. Se diseñó un novel procedimiento constructivo tipo GRASP y se aportaron dos variantes de PR (estática y dinámica). Todos los componentes de la metaheurística fueron ampliamente evaluados en instancias del problema de 5000 BUs. Cabe destacar que los métodos exactos apenas resuelven problemas de 50-80 BUs.
Los resultados experimentales mostraron que el procedimiento constructivo propuesto es capaz de generar soluciones de muy buena calidad. También se observó que la búsqueda local de GPR-CTDP mejora notablemente las soluciones construídas en términos de su calidad (función de dispersión) y del balance territorial. Los resultados también indicaron que ambas estrategias de PR ayudaron en forma impactante a mejorar aún más la calidad de las soluciones obtenidas con el procedimiento constructivo y la búsqueda local, con- firmando el excelente desempeño de la combinación GRASP-PR. En particular, se observó que mejores soluciones se obtienen con la versión estática de PR.
AGRADECIMIENTOS
Esta investigación fue apoyada por el Conacyt (apoyos CB-2005-01/48499-Y, CB- 2011-01/166397 y CB- 241306), UANL-Paicyt (apoyos CE012-09, IT511-10 y CE728-11) y Promep (apoyo 103.5/11/4330).
*Universidad Autónoma de Nuevo León.
**Instituto Nacional de Astrofísica, Óptica y Electrónica.
Contacto: roger.rios@uanl.edu.mx
REFERENCIAS
Elizondo-Amaya, M.G., Ríos-Mercado, R.Z., y Díaz, J.A. (2014). A dual bounding scheme for a territory design problem. Annals of Operations Research, 44:193- 205.
Feo, T.A. y Resende, M.G.C. (1995). Greedy randomized adaptive search procedures. J. of Global Optimization, 6(2):109-133.
Glover, F. (1996). Tabu search and adaptive memory programming-Advances, applications, and challenges. En R.S. Barr, R.V. Helgason y J.L Kennington (editors), Interfaces in Computer Science and Operations Research, capítulo 1, pp. 1-75. Kluwer, Dordrecht, Holanda.
Kalcsics, J., Nickel, S., y Schröder, M. (2005). Towards a unified territorial design approach: Applications, algorithms, and GIS integration. TOP, 13(1):1-56.
Resende, M.G.C., et al. (2010). GRASP and path relinking for the max-min diversity problem. Computers & Operations Research, 37(3):498-508.
Ribeiro, C.C., Uchoa, E., y Werneck, R.F. (2002). A hybrid GRASP with perturbations for the Steiner problem in graphs. INFORMS J. on Computing, 14(3):228-246.
Ríos-Mercado, R.Z., y Escalante, H.J. (2016). GRASP with path relinking for commercial districting. Expert Systems with Applications, 44:102-113.
Ríos-Mercado, R.Z., y Fernández, E. (2009). A reactive GRASP for a commercial territory design problem with multiple balancing requirements. Computers & Operations Research, 36(3):755-776.
Ríos-Mercado, R.Z., y López-Pérez, J.F. (2013). Commercial territory design planning with realignment and disjoint assignment requirements. Omega, 41(3):525- 535.
Salazar-Aguilar, M.A., Ríos-Mercado, R.Z., y Cabrera-Ríos, M. (2011). New models for commercial territory design. Networks & Spatial Economics, 11(3):487- 507.
Salazar-Aguilar, M.A., et al. (2012). Multiobjective scatter search for a commercial territory design problem. Annals of Operations Reseach, 199(1):343-360.
Recibido: 8 de septiembre de 2017
Aceptado: 13 de octubre de 2017