Solución de la ecuación algebraica de Riccati
DOI:
https://doi.org/10.29105/cienciauanl27.127-5Palabras clave:
ecuación algebraica de Riccati, matriz por bloques, valores propios, vectores propios, diagonalizaciónResumen
En este trabajo se obtiene un conjunto de soluciones para la ecuación algebraica de Riccati (ARE), la cual es expresada en términos de los coeficientes de la ecuación original sin necesidad de conocer una de las soluciones para, a partir de ésta, obtener la segunda, como se hace en el caso de la ecuación de Bernoulli. Las soluciones son obtenidas partiendo de una matriz simétrica S por bloques, formada con los coeficientes de la ARE. Las soluciones de la ARE son obtenidas partiendo del cálculo de los valores propios de S y aplicando los principios de ortogonalidad en una base de un módulo sobre el anillo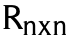 
. Este procedimiento supone condiciones de simetría en los coeficientes de la ARE y se considera que la diagonalización de la matriz por bloques S siempre es posible. La metodología propuesta se muestra en dos ejemplos.
Descargas
Citas
Adam, C. (2000). Continuity of the solution of the Riccati equations for continuous time JLQP, IEEE Transactions on Automatic Control, 45(5), 934-937. DOI: https://doi.org/10.1109/9.855554
Alam, K.N., Ara, A., y Jamil, M. (2011). An efficient approach for solving the Riccati equation with fractional orders, in Elsevier (ed.), Computers & Mathematics with Applications, Elsevier, 2683-2689. DOI: https://doi.org/10.1016/j.camwa.2011.03.017
Barabanov, N.E., y Ortega R. (2004). On the solvability of extended Riccati equations, IEEE Transactions on Automatic Control, 49(4), 598-602. DOI: https://doi.org/10.1109/TAC.2004.825628
Boyce, W.E., DiPrima, R.C. (2012). Elementary Differential Equations and Boundary Value Problems, John Wiley & Sons.
Cai, X., Ding, Y. S., y Li, S.Y. (2017). Convergent properties of Riccati equation with application to stability analysis of state estimation, Hindawi Athematical Problems in Engineering, 2017, 1-7. DOI: https://doi.org/10.1155/2017/2367042
Carpanese, N. (2000). Periodic Riccati difference equations: Approaching equilibria by implicit systems, IEEE Transactions on Automatic Control, 45(7), 1391-1396. DOI: https://doi.org/10.1109/9.867066
Dennis, G., y Wright, Zill. (2012). Elementary Differential Equations and Boundary Value Problems, John Wiley & Sons.
Freiling, G., Lee, S.R., y Jank, G. (1998). Coupled Matrix Riccati Equations in Minimal Cost Variance Control Problems, IEEE Transactions on Automatic Control, 4(3), 556-560.
Hench, J.J., He, C., Kvucera, V., et al. (1998). Coupled matrix Riccati equations in minimal cost variance control problems, IEEE Transactions on Automatic Control, 44(3), 556-560. DOI: https://doi.org/10.1109/9.751349
Jiménez, J.A. (2015). La solución de algunas EDO de Riccati, Revista Digital Matemática, Educación e Internet, 15(2). DOI: https://doi.org/10.18845/rdmei.v15i2.2170
Nguyen, T., y Gajic, Z. (2010). Solving the matrix differential Riccati equation: A Lyapunov equation approach, IEEE Transactions on Automatic Control, 55(1), 191-194. https://doi.org/10.1109/TAC.2009.2033841 DOI: https://doi.org/10.1109/TAC.2009.2033841
Petkov, P., Christov, N., y Konstantinov, M. (1991). Computational Methods for Linear Control Systems, Prentice, New York.
Rojas, A.J. (2021). Modified Algebraic Riccati Equation Closed-Form Stabilizing Solution, IEEE Access, 9, 140667-140675. https://doi.org/10.1109/ACCESS.2021.3119592 DOI: https://doi.org/10.1109/ACCESS.2021.3119592
Reid, W.T. (1972). Riccati differential equations, Academic Press.
Shirilord, Akbar, Dehghan, Mehdi, (2022). Closed-form solution of non-symmetric algebraic Riccati matrix equation, Applied Mathematics Letters, 131, https://doi.org/10.1016/j.aml.2022.108040 DOI: https://doi.org/10.1016/j.aml.2022.108040
Wu, Ai-Guo, Sun, Hui-Jie, Zhang, Ying, (2020). A novel iterative algorithm for solving coupled Riccati equations, Applied Mathematics and Computation, 364, https://doi.org/10.1016/j.amc.2019.124645 DOI: https://doi.org/10.1016/j.amc.2019.124645
Zhang, L., Chen, M.Z.Q., Gao, Z., et al. (2024). On the explicit Hermitian solutions of the continuous-time algebraic Riccati matrix equation for controllable systems, IET Control Theory Appl, 1-12, https://doi.org/10.1049/cth2.12618 DOI: https://doi.org/10.1049/cth2.12618
Zoran, Gajic, Djordjija, Petkovski, Xuemin, Shen. (2017). Singularly perturbed and weakly coupled linear control systems, a recursive approach, Technical report, Springer Nature Switzerland AG.
