SOBRE EL ANÁLISIS DE LA FORMA DE LOS DATOS: UN NUEVO PARADIGMA EN CIENCIA DE DATOS

Jesús Francisco Espinoza Fierro*, Yitzhak David Gutiérrez Moya*,
Rosalía Guadalupe Hernández Amador*

CIENCIA UANL / AÑO 22, No.96 julio-agosto 2019

https://doi.org/10.29105/cienciauanl22.96-4

 

RESUMEN

La ciencia de datos es un área multidisciplinaria en la que convergen herramientas de estadística, cómputo científico, matemáticas puras y un profundo entendimiento del contexto del problema a estudiar. Dentro de esta área han surgido recientes investigaciones en las que el análisis se enfoca en un aspecto más cualitativo del estudio, a saber: la forma de los datos. En el presente trabajo describimos esquemáticamente algunas de las herramientas para implementar dicho análisis y presentamos como propuesta un algoritmo eficiente, auxiliar en el estudio de estructuras de baja dimensión simplicial, inmersas en un espacio de representabilidad de dimensión alta.

Palabras clave: análisis topológico de datos, complejo de Vietoris-Rips, complejo de Cech, bola minimal.

ABSTRACT

Data science is a multidisciplinary area in which statistics, scientific computation, pure mathematics and adeep understanding of the context of the problem to be studied converge. Within this area, recent studies have emerged in which the analysis centers on a qualitative aspect of the study, the form of the data. In the present research some of the tools to schematically implementthis analysis are described, and an efficient algorithm tothe study of low dimensional structures, immersed in a high dimension representability space is proposed.

Keywords: topological data analysis, Vietoris-Rips complex, Cech complex, miniball problem.

Dentro de las matemáticas, diversas áreas han sido tradicionalmente consideradas como puras (o básicas), entre las que se destaca la topología, por considerarse una de las “geometrías más elementales”, encargada de estudiar la forma de ciertos objetos, así como las propiedades que se preservan al deformarlos continuamente, es decir, sin rompimientos ni pegaduras. Las recientes aplicaciones que ésta ha tenido junto con el álgebra, así como la impresionante integración con áreas como la combinatoria, la probabilidad, la estadística y el cómputo científico, han propiciado la consolidación de una interesante área llamada análisis topológico de datos (ATD); puede consultarse Zomorodian (2012) para una introducción al tema, y Otter et al. (2017) para una exposición panorámica, alcances del ATD y su implementación computacional.

Debido al amplio espectro de tópicos en donde se ha implementado (Piangerelli et al., 2018; Pranav et al., 2017; Taylor et al.,2015; Nicolau, Levine y Carlsson, 2011), el ATD ha revolucionado viejos paradigmas, posicionándose como una herramienta sólida y estable para abordar el análisis de complejas estructuras de nubes de datos y consolidándose como un importante recurso para el entendimiento de estructuras geométricas de dimensiones superiores.

Esquemáticamente, el ATD consiste en el uso de las técnicas de la topología y el álgebra para el análisis de nubes de puntos (datos) en donde existe una noción de cercanía, dotando primero a éstos con una familia de estructuras geométricas (filtración simplicial). Luego, mediante distintas herramientas del álgebra lineal, se realiza el cálculo de lo que en topología algebraica es conocido como homología persistente (definida en 2002 por Edelsbrunner, Letscher y Zomorodian) y que consiste de una familia de espacios vectoriales apropiadamente construidos; tal estructura algebraica es representada gráficamente en un código de barras o en un diagrama de persistencia (Carlsson et al., 2004). Dependiendo de la manera en la que se construye la estructura simplicial filtrada, se tiene una correspondiente interpretación de lo que el código de barras está detectando.

Cada uno de los pasos del ATD señalado en la figura 1 representa un área de investigación actualmente activa, y entrar en mayores detalles escapa de los objetivos del presente escrito, por lo que nos enfocaremos en la primera parte del ATD: la construcción de una estructura simplicial filtrada asociada a una nube de puntos (los datos). Identificar la estructura adecuada con la cual dotar de geometría a los datos es uno de los aspectos clave y no triviales para realizar el análisis.

LA FORMA DE LOS DATOS

El ATD se realiza bajo la hipótesis de que los datos encajan en cierto modelo salvo ruido, esto es, que existe una estructura geométrica y el correspondiente sistema de ecuaciones que la modela, de donde los datos han sido muestreados salvo cierto ruido, y es tarea del ATD inferir dicho espacio mediante la detección de ciertas características relativas a su forma. Por ejemplo,en la figura 2 se muestran tres nubes de puntos representadasen el plano. Intuitivamente podemos inferir la geometría del modelo subyacente en cada caso: en la nube de puntos de la izquierda, la experiencia dicta utilizar un modelo de regresión lineal; para las otras dos nubes de puntos, es claro que el espacio subyacente no tiene una estructura lineal, más bien del tipo periódico para la gráfica del centro y de agrupamiento para la gráfica de la derecha.

DISTINTAS GEOMETRÍAS SOBRE UNA NUBE DE PUNTOS

El complejo simplicial de Vietoris-Rips

Dada una nube de puntos N={?1,…,?ⁿ
} en un espacio métrico y un parámetro de proximidad ε ≥0, una manera usual de asociar una estructura geométrica (o combinatoria) a N, es construir la gráfica cuyo conjunto de vértices N₀ consta de todos los subconjuntos unitarios {?ᵢ } de N, y el conjunto de aristas N₁ consiste de los subconjuntos de N con dos elementos {?_i, ?_j} ⊂ N que satisfacen que la distancia entre ambos puntos es menor o igual que ε. Podemos considerar a ésta como una estructura de dimensión simplicial 1. Para construir una estructura geométrica de mayor dimensión simplicial, definimos por cada número natural k≥0 el conjunto N_k dado por la colección de todos los subconjuntos con k + 1 elementos {?i₀,…, ?i_k } ⊂ N que satisfacen que la distancia entre cada par de elementos es menor o igual que ε. El complejo simplicial de Vietoris-Rips VR (N,ε) es la unión de todos los N? (Ghrist, 2007, p. 63), y la dimensión simplicial de este complejo corresponde al valor máximo de k tal que N_k es no vacío. Los elementos en N_k son llamados k-simplejos de Vietoris-Rips.

Notemos que si la nube de puntos pertenece a un espacio euclidiano N ⊂ ℝᵈ, entonces la estructura simplicial de Vietoris-RipsVR(N, ε) puede reformularse en términos debolas en ℝᵈ de la siguiente manera: σ ∈ VR(N,ε) si y sólo si B(xᵢ, ε⁄2)∩B(x_j, ε⁄2)≠∅ para todos x_i, x_j∈σ, donde B(x,r) ={y ∈ ℝᵈ: dist(?,y)⩽r} y dist representa la distancia euclidiana. Equivalentemente, σ∈VR(N,ε) si y sólo si su diámetro diam(σ)=máx{dist(?_i, ?_j ):?_i, ?_j ∈σ} es menor o igual que ε.

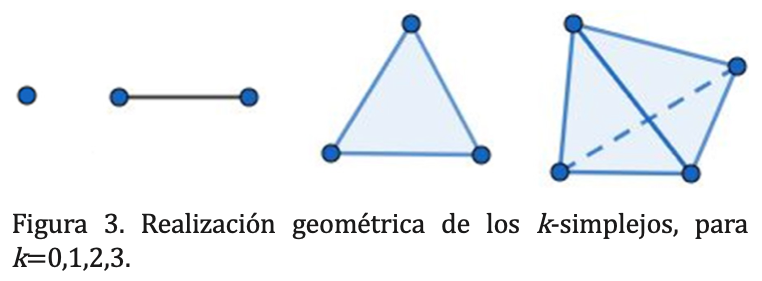
En este contexto, un k-simplejo σ={?i₀,…, ?i_k } ∈ VR (N,ε), cuyos puntos están en posición general, puede identificarse con la envolvente convexaΔ[?i₀,…, ?i_k ] del conjunto σ ⊂ ℝᵈ, esto es, el mínimo subconjunto convexo enℝᵈ que contiene a σ. El conjunto Δ[?i₀,…, ?i_k ] es llamado una realización geométrica del k-simplejo σ = {?i₀,…, ?i_k }. Para valores pequeños de k es posible visualizar tales realizaciones geométricas como se muestra en la figura 3, donde la realización geométrica de un 0-simplejo corresponde a un punto, la de un 1-simplejo a un segmento de línea, la de un 2-simplejo a un triángulo y la de un 3-simplejo a un tetraedro.

El complejo simplicial de Cech

La siguiente estructura simplicial, definida también para una nube de puntos N ⊂ ℝ^d y un parámetro de proximidad ε≥0, es llamada complejo de Cech, denotada por C(N,ε), y es una variante del complejo de Vietoris-Rips que es de hecho una representación más fiel de la geometría subyacente de los datos (Ghrist, 2007, p. 63). Los k-simplejos de Cech son definidos de la siguiente manera: σ={?i₀,…, ?i_k} ∈ C(N,ε) si y sólo si B(?i₀,ε⁄2)∩…∩B(?i_k,ε⁄2)≠∅. En equivalencia, σ ∈ C(N,ε) si puede acotarse por una bola de diámetro menor o igual que ε. Podemos observar que los 0-simplejos y los 1-simplejos de Cech coinciden con los de Vietoris-Rips. Para k≥2 todo k-simplejo σ∈C(N,ε) satisface que σ∈VR(N,ε), es decir, C(N,ε) ⊂VR(N,ε), pero la contención es propia en general. Este cambio en la definición de los k-simplejos de Cech con respecto a la estructura de Vietoris-Rips tiene importantes implicaciones en los costos computacionales al momento de construir la estructura simplicial, aun cuando la estructura simplicial de Cech tiene en general una menor cantidad de simplejos que la de Vietoris-Rips (pues para su construcción se debe analizar el subconjunto formado por la intersección de bolas). Sin embargo, su uso está justificado por ser una representación más fiel de la geometría subyacente de los datos (Ghrist, 2007, p. 63). Además, la estructura simplicial de Cech aparece de manera natural en distintos estudios, como el análisis de redes (Yuchen, Jialiang y Martins, 2018; Le et al., 2017).

ESTRUCTURA FILTRADA DE CECH Y EL PROBLEMA DE LA BOLA MINIMAL

Como comentamos en la sección anterior, para determinar siσ={?i₀,…, ?i_k} es un simplejo en la estructura de Cech C(N,ε), basta con comprobar la existencia de una bola de diámetro ε que encierre al subconjunto σ ⊂ ℝᵈ. Es claro que, para distintos valores del parámetro de proximidad, tenemos distintas estructuras simpliciales asociadas, como podemos ver en la figura 4, donde cada vértice corresponde a la ubicación de cada una de las antenas:

El enfoque que aborda el ATD consiste en no fijar un valor para el parámetro de proximidad ε, sino considerar todos los valores del parámetro en cierto rango junto con las correspondientes estructuras simpliciales generadas, a fin de identificar aquellas propiedades geométricas que más persisten a través de esta familia.

Es claro que si ε1⩽ε₂, entonces C(N,ε₁) ⊂ C(N,ε₂). Debido a esta propiedad, la estructura simplicial de Cech tiene una estructura filtrada de manera natural: C(N,ε₀=0) ⊂ C(N,ε₁) ⊂…⊂ C(N,εʟ=ε). Podemos reescribir C(N,εᵢ) ={σ ∈ C(N,ε): diam(M-B(σ))⩽εᵢ}, donde MB(σ) ⊂ ℝᵈ denota la bola de radio mínimo que acota al subconjunto finito σ, de modo que el estudio de la estructura simplicial filtrada de Cech está íntimamente relacionado con el problema de determinar la bola minimal para colecciones de puntos σ={?i₀,…, ?i_k} con k⩽n. Encontrar el centro y radio mínimo de la bola que acote una colección finita de puntos σ ⊂ ℝᵈ es conocido como el problema de la bola minimal (miniball problem, en inglés). Este problema ha sido resuelto usando técnicas muy variadas (Fischer, Gärtner y Kutz, 2003; Gärtner, 1999).

UN ALGORITMO PARA EL CÁLCULO DE LA BOLA MINIMAL

En esta sección presentamos dos algoritmos ad hoc para calcular la bola minimal para colecciones de tres o cuatro puntos σ, en un espacio euclidiano de dimensión arbitraria. El punto clave de los algoritmos consiste en identificar cuándo la bola minimal coincide con una bola circunscrita a σ, o bien a un subconjunto de σ en específico. En la siguiente sección mostraremos la comparación en tiempos con respecto al algoritmo dado por Fischer, Gärtner y Kutz (2003), que puede manejar eficientemente conjuntos arbitrarios de puntos en dimensiones altas. Nos referiremos a tal algoritmo como “minibola”. Los algoritmos propuestos en este trabajo, llamados MB₃ y MB₄, reciben una colección de tres y cuatro puntos, respectivamente, y calculan la bola minimal MB(σ) que acota a σ.

Colecciones de tres puntos

Para una colección de tres puntos σ ⊂ ℝᵈ sólo se presentan dos casos para MB(σ): (i) cuando la bola minimal coincide con la bola circunscrita CB([?₁,?₂]) de los dos puntos más separados ?₁ y ?₂, (ii) cuando coincide con la bola circunscrita del triángulo formado por los tres puntos CB([?₁,?₂,?₃]). Para poder distinguir qué caso debe usarse para el cálculo de la bola minimal, sólo es necesario verificar el signo del producto escalar ⟨?₁-?₃,?₂-?₃⟩; en cualquiera de los dos casos, el problema de encontrar la bola circunscrita se puede resolver con fórmulas explícitas (Gutiérrez-Moya, 2018). Esquemáticamente, el algoritmo queda descrito como sigue:

Algoritmo MB₃ 
Entrada: tres puntos σ = {?₁,?₂,?₃} ⊂ ℝᵈ en el espacio euclidiano de dimensión d. 
Salida: la bola minimal MB(σ). 
1. Renombrar los puntos de σ={?₁,?₂,?₃} de tal forma que dist(?₁,?₂)=diam(σ). 
2. Si ⟨?₁-?₃,?₂-?₃⟩ ≤ 0, entonces
                 MB(σ)=CB([?₁,?₂,?₃]),
en otro caso MB(σ)=CB([?₁,?₂,?₃]). 
3. Regresar MB(σ).

Colecciones de cuatro puntos

El algoritmo MB₄ recibe una colección de cuatro puntosσ={?₁,?₂,?₃,?₄} ⊂ ℝᵈ, y proporciona la bola minimal que acota σ. En este caso, la bola minimal corresponde a la bola circunscrita de alguno de los siguientes conjuntos: (i) los puntos más alejados, (ii) los vértices de alguna de las cuatro caras (triángulos) del tetraedro formado por σ, (iii) el tetraedro Δ[?₁,?₂,?₃,?₄]. De modo que, esencialmente, el algoritmo MB₄ consiste en iterar el algoritmo MB₃ para subconjuntos de tres puntos. Esto implica que su tiempo de cómputo sea proporcional al del algoritmo MB₃. Más explícitamente, el algoritmo MB₄ tiene el siguiente pseudocódigo.

Algoritmo MB₄ 
Entrada: cuatro puntos σ={?₁,?₂,?₃,?₄} ⊂ ℝᵈ en el espacio
euclidiano de dimensión d. 
Salida: la bola minimal MB(σ). 
1.Renombrar los puntos de σ={?₁,?₂,?₃,?₄} de tal forma
que dist(?₁,?₂)=diam(σ). 
2. Si ⟨?₁-?₃,?₂-?₃⟩≤0 y ⟨?₁–?₄, ?₂–?₄⟩≤0 entonces 
                 MB(σ)=CB([?₁,?₂]),
                 ir al Paso (3)      
   en otro caso   
                 para i=1 hasta i=4 hacer
                 definir Nᵢ=σ –?ᵢ
                 si xᵢ ∈ MB(Nᵢ) entonces
                                  MB(σ)=MB(Nᵢ)
                                  ir al Paso (3)
                fin para
                calcular MB(σ)=CB([?₁,?₂,?₃,?₄])
3. Regresar MB(σ).

Es importante mencionar que en la codificación (en C++) del algoritmo MB₄ es posible reutilizar varios de los cálculos necesarios para las iteraciones en el paso 2; además, todos los productos escalares pueden ser calculados a partir de las distancias entre los puntos en σ. Lo anterior impacta significativamente en la disminución de los tiempos de cómputo en dimensiones altas.

EXPERIMENTACIÓN COMPUTACIONAL

A continuación, presentamos una comparación entre los tiempos de cómputo de los algoritmos MB₃ y MB₄, con respecto al algoritmo propuesto por Fischer, Gärtner y Kutz (2003) al que nos referimos por “minibola”; todos codificados en el lenguaje C++. En la gráfica de arriba de la figura 5 se muestran los tiempos promedio de ejecución de los algoritmos MB₃ y minibola, con respecto a la dimensión del espacio ambiente; en la gráfica de abajo se comparan los tiempos promedio de MB₄ y minibola.

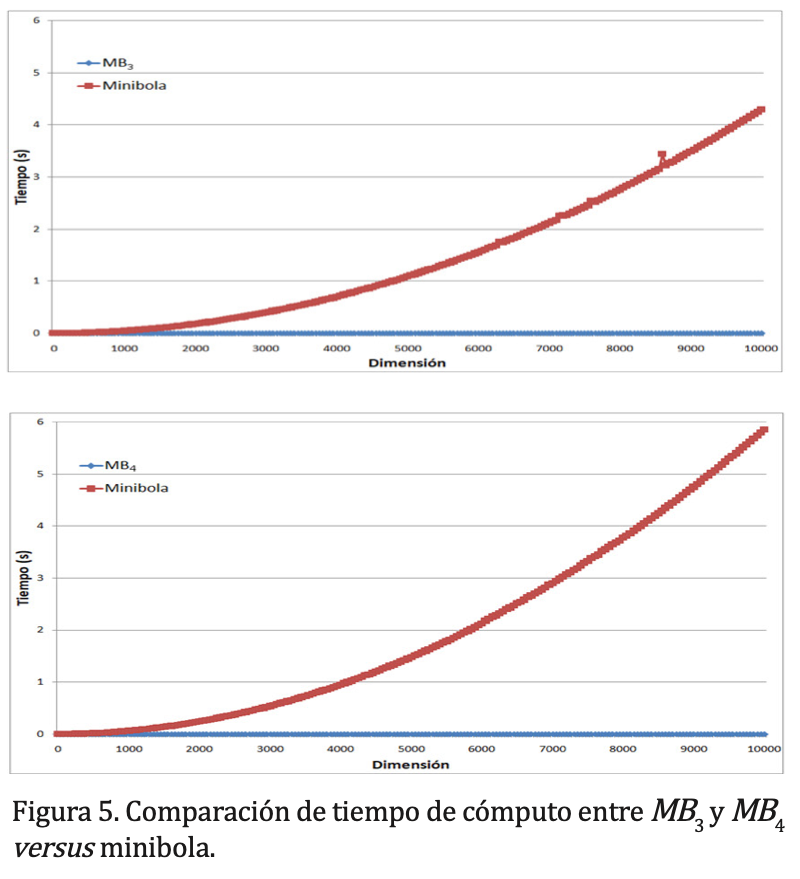
La experimentación computacional se realizó sobre espacios euclidianos de dimensión d=50k, con k=1,2,…,200. Para cada uno de tales valores d se generaron 10,000 nubes de puntos {?₁,?₂,?₃} ⊂ ℝᵈ, donde cada ?ᵢ ∈ ℝᵈ consiste de d números en el intervalo [0,10] elegidos aleatoriamente, y se calcularon los correspondientes tiempos promedio de ejecución de MB₃ y minibola; y análogamente para la comparación entre los algoritmos MB₄ y minibola.

Los cálculos se realizaron ejecutando un proceso por cada hilo sobre un procesador Intel Xeon E5-2698v4 a 2.2 GHz. El uso de memoria RAM fue mínimo. La experimentación muestra que el algoritmo minibola es de orden cuadrático, lo cual es consistente con lo presentado en Fischer, Gärtner y Kutz (2003). Por otro lado, los algoritmos MB₃ y MB₄ son de orden lineal y el tiempo promedio de cómputo es del orden 10⁻⁵,   aproximadamente. Tanto los fundamentos matemáticos como los códigos en C++ de este trabajo pueden consultarse en Gutiérrez-Moya, 2018.

CONCLUSIÓN

En la primera parte de este trabajo describimos cómo puede dotarse de distintas geometrías a una base de datos, vista como una nube de puntos, mediante dos de las estructuras más usuales: los complejos simpliciales de Vietoris-Rips y de Cech. Posteriormente enunciamos el problema de la bola minimal y comentamos su relevancia para la construcción de la filtración del complejode Cech. Concluimos con la propuesta de dos algoritmos MB₃ y MB₄, cuyas complejidades son de orden lineal y que permiten calcular los simplejos de Cech de dimensión simplicial dos y tres de manera sumamente eficiente, aun cuando la nube de puntos pertenece a un espacio euclidiano de dimensión alta.

La desventaja de los algoritmos MB₃ y MB₄ es que no son adecuados para generalizarse a dimensión simplicial arbitraria. Aun cuando la codificación en el lenguaje de programación se vuelve bastante sofisticada, realmente el obstáculo principal radica en la complejidad algorítmica. Por ejemplo, si construimos el algoritmo MB₅ siguiendo la misma metodología que para MB₃ y MB₄, entonces tal algoritmo iteraría cinco veces al algoritmo MB₄, el cual, a su vez, itera cuatro veces a MB₃; en general, MB? estaría iterando n⋅(n – 1)⋅…⋅4 veces a MB₃ y la eficiencia que se mostró en la sección relativa a la experimentación computacional se vería significativamente disminuida, incluso para valores de n no muy grandes.

Por otro lado, aunque una gran cantidad de los datos que se generan actualmente en nuestra sociedad son de naturaleza altamente multidimensional, los aspectos que suelen estudiarse en una primera instancia en el análisis topológico de datos son los relativos a la clasificación (análisis de clúster) y si la variabilidad de los datos puede ser representada significativamente mediante un modelo periódico de baja dimensión simplicial. Sin embargo, un análisis topológico de una base de datos multivariada que requiera una estructura simplicial de Cech tendrá, en general, una cantidad considerable de k-simplejos de Cech y su análisis mediante las librerías usuales será computacionalmente costoso, es aquí donde radica la importancia para el ATD de contar con algoritmos eficientes como MB₃ y MB₄.

AGRADECIMIENTOS

El presente trabajo fue desarrollado gracias al apoyo y financiamiento del Prodep a través del Proyecto “Métodos de topología combinatoria en el análisis de datos” (511-6/17-7715). Los autores agradecen al Área de Cómputo de Alto Rendimiento de la Universidad de Sonora (ACARUS) por el apoyo proporcionado para el uso de su infraestructura de supercómputo.

* Universidad de Sonora.
Contacto: jesus.espinoza@mat.uson.mx

REFERENCIAS

Carlsson, G., Zomorodian, A., Collins, A., et al. (2004). Persistence barcodes for shapes. Proceedings of the 2004 Euro-graphics/ACM SIGGRAPH symposium on Geometry processing-SGP’04. pp. 124-135. DOI:10.1145/1057432.1057449. 
Fischer, K., Gärtner, B. y Kutz, M. (2003). Fast Smallest-Enclosing-Ball Computation in High Dimensions. Algorithms-ESA 2003. pp. 630-641. DOI:10.1007/978-3-540- 39658-1_57. 
Gärtner, B. (1999). Fast and Robust Smallest Enclosing Balls. AlgorithmsESA’99. pp. 325-338. DOI:10.1007/3- 540-48481-7_29. 
Ghrist, R. (2007). Barcodes: The persistent topology of data. Bulletin of the American Mathematical Society. 45(1): 61- 75. DOI:10.1090/s0273-0979-07-01191-3. 
Gutiérrez-Moya, Y. (2018). Complejo simplicial de Čech debaja dimensión: Un algoritmo ad hoc para su construcción. Universidad de Sonora, Tesis de Licenciatura. URL http://lic.mat.uson.mx  
Le, N., Vergne, A., Martins, P., et al. (2017). Optimizewireless networks for energy saving by distributedcomputation of Čech complex. 2017 IEEE 13th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob). DOI:10.1109/WiMOB.2017.8115760. 
Nicolau, M., Levine, A. y Carlsson, G. (2011). Topology based data analysis identifies a subgroup of breast cancers with a unique mutational profile and excellent survival. Proceedings of the National Academy of Sciences. 108(17): 7265-7270. DOI:10.1073/pnas.1102826108. 
Otter, N., Porter, M.A., Tillmann, U., et al. (2017). A roadmap for the computation of persistent homology. EPJ Data Science. 6(17). DOI:10.1140/epjds/s13688-017- 0109-5. 
Piangerelli, M., Rucco, M., Tesei, L., et al. (2018). Topological classifier for detecting the emergence of epileptic seizures. BMC Res Notes. 11:392. DOI:10.1186/ s13104-018-3482-7.  
Pranav, P., Edelsbrunner, H., van de Weygaert, R., et al.(2017). The topology of the cosmic web in terms of persistent Betti numbers. Monthly Notices of the Royal Astronomical Society. 465(4): 4281-4310. DOI:10.1093/ mnras/stw2862. 
Taylor, D., Klimm, F., Harrington, H., et al. (2015). Topological data analysis of contagion maps for examining spreading processes on networks. Nature Communications. 6(1). DOI: 10.1038/ncomms8723. 
Yuchen, W., Jialiang, L. y Martins, P. (2018). Distributed Coverage Hole Detection Algorithm Based on ČechComplex. Communications and Networking. pp. 165- 175. DOI:10.1007/978-3-319-78139-6_17.  
Zomorodian, A. (2012). Topological Data Analysis. In:A. Zomorodian (ed.), Advances in Applied and Computational Topology. Providence, Rhode Island: American Mathematical Society. pp. 1-39. DOI:10.1090/psa-pm/070.

RECIBIDO: 02/07/2018
ACEPT