CÁLCULO DE REGIONES DE ESTABILIDAD ROBUSTA PARA SISTEMAS INCIERTOS MEDIANTE HERRAMIENTAS DE POSITIVIDAD DE FUNCIONES

Mario Alberto López Vega*, César Elizondo González*, 
Cornelio Posadas Castillo*, Efraín Alcorta García*

CIENCIA UANL / AÑO 22, No.96 julio-agosto 2019

https://doi.org/10.29105/cienciauanl22.96-1

 

RESUMEN

En este trabajo se propone un algoritmo para el diseño de un controlador de sistemas lineales con incertidumbre paramétrica. El punto de partida es una herramienta matemática para la solución de problemas de positividad de funciones multivariables polinómicas. El algoritmo propuesto está basado en un resultado para la estabilidad de sistemas lineales invariantes en el tiempo (Linear Time Invariant, LTI) con incertidumbre en sus parámetros. El algoritmo permite encontrar una familia de controladores que garantizan estabilidad robustamente. La solución propuesta, así como sus ventajas, son mostradas mediante un ejemplo.

Palabras clave: positividad, estabilidad robusta, polinomio característico, controlador, sistema lineal.

ABSTRACT

An algorithm for the design of a linear systems controller with parametric uncertainty is proposed. The starting point is a mathematical tool for the solution of positivity problems of multivariate polynomial functions. The proposed algorithm is based on a result for the stability of Linear Time Invariant (LTI) systems with uncertainty inits parameters. The algorithm allows finding a family ofcontrollers that guarantee stability robustly. The proposed solution, as well as its advantages, are shown by an example.

Keywords: positivity, robust stability, characteristic polynomial, controller, linear system.

Sistemas industriales son frecuentemente modelados mediante ecuaciones diferenciales con la finalidad de diseñar controladores que permitan llevar las variables requeridas del proceso a niveles deseados. Desde el punto de vista práctico, los parámetros asociados al modelo no se pueden conocer con precisión y, generalmente, hay al menos algunos de estos parámetros que serán especificados a pertenecer a un intervalo de valores. Esto es conocido como incertidumbre paramétrica y representa un problema tanto para el análisis como para el diseño de sistemas de control.

El problema de estabilidad robusta con incertidumbre paramétrica no es un problema nuevo, existen varios enfoques que buscan mejorar el diseño de controladores robustos y las técnicas de modelado (Ackermann y Bartlett, 1993; Barmish, 1994; Bhattacharyya, Datta y Keel, 2009).

Ackermann y Bartlett (1993) proponen un esquema en el espacio de parámetros que resulta impráctico para un número de parámetros mayor. Barmish (1994) muestra una serie de herramientas que permiten análisis, pero no presenta un método sistemático de diseño. La propuesta más actual para solucionar el problema de diseño fue presentada por Bhattacharyya y su grupo (Bhattacharyya, Datta y Keel, 2009; Keel y Bhattacharyya, 2008; Knap, Keel y Bhattacharyya, 2011), donde se propone el diseño robusto de contro- ladores PID para sistemas lineales a partir de datos entrada-salida. Por un lado, no requiere el modelo de forma explícita, pero por otro sólo se considera controladores PID.

En este tipo de problema se parte de un sistema nominal estable, es decir, con parámetros fijos, y después se analiza la incertidumbre en los parámetros del sistema o las cotas de dichos parámetros. La solución radica en saber si el sistema con incertidumbre es o no estable en el intervalo de valores que lo integran. Claramente, en esta formulación, el sistema nominal es un miembro dentro de las cotas preestablecidas. En otras palabras, se tiene una familia de sistemas en el dominio del tiempo y el sistema nominal es miembro de esa familia de sistemas (Yedavalli, 2013).

El considerar la presencia de la incertidumbre en el diseño de controladores robustos sin sacrificar el desempeño del sistema es todo un reto. Existen diversas estrategias que enfrentan la incertidumbre paramétrica en el diseño de controladores (Mohsenizadeh, Keel y Bhattacharyya, 2014; Mercader y Banos, 2017).

En este trabajo se propone una solución para el diseño de controladores de sistemas lineales invariantes en el tiempo que tienen incertidumbre paramétrica. La propuesta está basada en resultados previos del grupo. Debido a la naturaleza del problema, se obtiene una familia de controladores que satisfacen robustamente el requisito de estabilidad. El resultado es mostrado mediante un ejemplo.

El hecho de que se obtenga una familia de controladores representa una ventaja del enfoque propuesto, pues nos deja la libertad para buscar, dentro de esta familia, el controlador que, además, cumpla con un criterio adicional de desempeño.

Note que, aunque se requiere como dato el modelo de sistema, el resultado no se limita a una estructura de controlador dado, pudiendo ser utilizada de manera abierta o bien con diferentes tipos o estructuras de controladores.

El resto del trabajo está organizado como sigue: en la sección preliminares se presenta la herramienta matemática “Descomposición de signo”, disponible para analizar la positividad de funciones polinómicas multivariables, así como un resultado para determinar la estabilidad robusta de sistemas inciertos. En la siguiente sección se describe el resultado principal, es decir, el algoritmo para diseño de controladores. Un ejemplo de aplicación es presentado, en él se clarifican los diferentes aspectos discutidos a lo largo del trabajo. Finalmente se presentan las conclusiones.

PRELIMINARES

Descomposición de signo

Descomposición de signo es una herramienta matemática que mediante el análisis de puntos extremos permitedeterminar, en condiciones necesarias y suficientes, la positividad robusta de funciones multivariables polinómicas dependientes de parámetros.

Definición 1.  Sea  ?:?^ɭ →? una función continua y sea Q ⊂ P ⊂ ?^ɭ un subconjunto convexo, se dice que ?(q) tiene descomposición de signo en Q si existen dos funciones acotadas no-decrecientes ?_? (⋅) ≥ 0, ?_? (⋅) ≥ 0, tales que ?(q)=?_? (q)-?_? (q)∀q∈Q. Dichas funciones se llamarán: la parte positiva de la función ?_? (q) y la parte negativa de la función ?_? (q) (Elizondo, 1999; 2000).

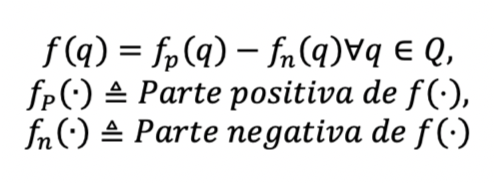
Representación (?? ,??)

Cuando una función continua ?:?^ɭ →? se descompone en Q ⊂ P ⊂ ?^ɭ, en sus partes positiva y negativa, ?_? (⋅) y ?_?  (⋅), realmente se está haciendo una transformación de ℝ^ɭ a ℝ² , la representación gráfica de la función en un plano (?_? ,?_?) es de utilidad para entender más fácilmente las propiedades que poseen las partes positiva y negativa de la función, para lo cual se establece la siguiente proposición. Si una función con descomposición de signo en Q es igual a cero para todo q elemento de Q, implica que ?_? (q)=?_?  (q) )∀q∈ Q, y su representación gráfica en el plano (?_?  (q),?_? (q)) es una línea recta a 45⁰ que contiene al origen, a la cual nos referiremos como la recta a 45⁰, los puntos arriba de ella corresponden a la representación gráfica de funciones con valor positivo y obviamente los de abajo a negativo.

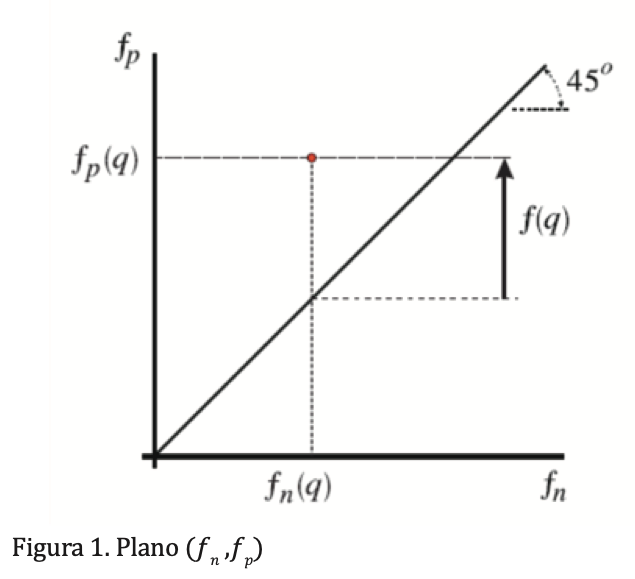
Debe notarse que independientemente del número de parámetros de la función multivariable polinómica, la función siempre será representada en ℝ² , representada en el plano  (?_?  (q), ?_? (q)) (figura 1).

Criterio de estabilidad de C. Elizondo

Este criterio de estabilidad presenta una tabla a partir de la cual se determina el número de raíces de un polinomio real que se encuentran en el semiplano derecho del plano complejo. Dicha tabla se fundamenta en el principio del argumento, índices de Cauchy, cadenas de Sturm ycadenas de Sturm modificadas. La tabla presenta algunas ventajas: las operaciones numéricas se reducen con respecto a otros criterios y los coeficientes son funciones multivariables polinómicas cuya positividad robustase obtiene en condiciones necesarias y suficientes utilizando descomposición de signo (Elizondo, 1999; 2000; 2001; 2011), determinando entonces la estabilidad robusta para sistemas LTI con incertidumbre paramétrica.

Teorema 2.3.1. Dado un polinomio ?(s)=C₀+C₁s+C₂ s ²+⋯+C_?-1s ^?-1+C_?s ^? con coeficientes reales, el número de raíces a la derecha del plano de los complejos es igual al número de variaciones de signo en la columna σ, en el siguiente arreglo (Elizondo, 2001).

La metodología de cálculo del signo σᵢ de un renglón es mucho más sencilla que lo que aparenta la expresión matemática que lo determina: el signo σᵢ de un renglón se determina multiplicando el signo de eᵢ,₁ por el signo del elemento inmediato superior a éste, es decir, el de e(ᵢ-₁),₁ y por los signos de los elementos superiores de la columna e «brincando» de dos en dos.

En el caso de que un elemento ℯ_i,1 sea cero, entonces se sustituye el cero por un ε>0 y se continúa el cálculo de la tabla. En caso de que todos los elementos ℯ_i,j de un renglón sean de valor cero, entonces se sustituye el renglón completo por la derivada del renglón superior.

Debe notarse que cada uno de los elementos ℯ_i,jfueron elaborados sin utilizar la división empleada en el criteriode Routh, por lo tanto los elementos ℯ_i,j en el caso de incertidumbre paramétrica son funciones multivariables polinómicas.

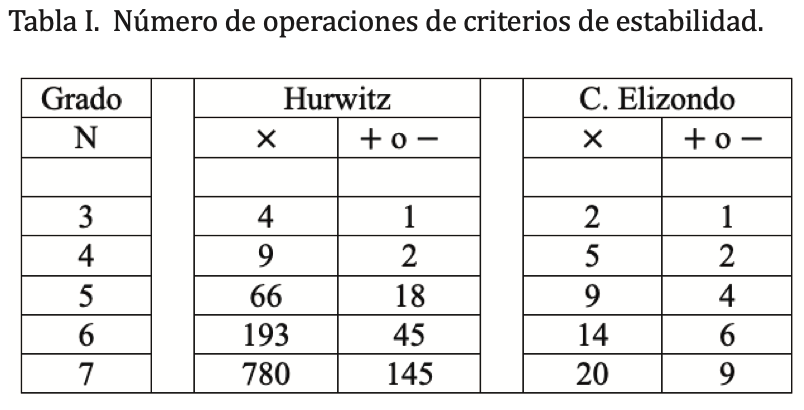
En la tabla I se muestra cómo el criterio Elizondo González tiene ventajas sobre el conocido criterio de Hurwitz.

METODOLOGÍA

Las herramientas matemáticas descritas anteriormente pueden aplicarse para encontrar una región de controladores PI que estabilizan a un sistema LTI con incertidumbre paramétrica.

Se considera cualquier sistema LTI en forma general con incertidumbre paramétrica en cascada con un controlador PI y retroalimentación unitaria. Se obtiene la función de transferencia correspondiente a la familia de sistemas y al conjunto de controladores PI generados por la incertidumbre paramétrica en lazo cerrado y a continuación se analiza el polinomio característico de la función de transferencia. Es importante establecer un porcentaje de incertidumbre para los parámetros de la planta, el polinomio característico a analizar es una función multivariable polinómica que depende de parámetros acotados, algunas de estas cotas pudiesen ser valores negativos. Por lo tanto, la “descomposición de signo” comienza con una transformación de coordenadas de los parámetros acotados a un conjunto de parámetros matemáticos tal que todos los vectores de los nuevos parámetros estén contenidos en un cono convexo positivo. Para agregar de manera sencilla un desempeño al conjunto de controladores que estabilizan una familia de sistemas, se desea que la parte real del polinomio característico esté dentro de una región definida por un segmento, generándose dos nuevos polinomios característicos a analizar. Usando el teorema de estabilidad relativa, se analizan la estabilidad robusta de los polinomios ?(s-a) y ?(-s-b). Entonces, la estabilidad robusta de cada polinomio ?(s-a) y ?(-s-b) será analizada utilizando el reciente criterio de estabilidad (Elizondo C., 2001), y aplicando “descomposición de signo” se probará la positividad robusta de los elementos ℯ_i,1. Si cada elemento ℯ_i,1 es robustamente positivo, entonces la columna entera será positiva y el polinomio del sistema analizado será robustamente estable. 

La metodología descrita anteriormente da una explicación del funcionamiento del resultado principal de este trabajo. A continuación se define el algoritmo capaz de establecer un conjunto de controladores robustos que dan estabilidad robusta a un sistema LTI con incertidumbre paramétrica en una región predeterminada.

RESULTADOS

A continuación se presenta el resultado principal de este artículo, un algoritmo que permite encontrar una familia de controladores que garantizan estabilidad robusta. Para una mejor comprensión del resultado principal, se definen las variables y términos utilizados a lo largo del algoritmo: K* (k₁*,k₂*): punto de partida del algoritmo en una región robustamente estable donde inicia la búsqueda de las cotas de los paramétros k₁^⬚   y k₂^⬚, respectivamente. 
ε: medida propuesta para analizar el tamaño de las cajas o regiones de estabilidad robusta. 
α: tolerancia que el algoritmo utiliza para finalizar y mostrar resultados. k?ʀʙ₁: primera cota lateral derecha para el parámetro k₁. 
k?ʀʙ₁: primera cota lateral izquierda para el parámetro k₁. 
ν₁: medida que indica el número de intervalos a analizar en el primer segmento encontrado (en función de la tolerancia ε). 
k*i2_em= cota mínima estimada para el parámetro k₂. 
k*i2_eM= cota máxima estimada para el parámetro k₂.
Aᵢ, Bᵢ , Cᵢ , Dᵢ = vértices definidos por los valores de las cotas laterales y las cotas inferior y superior.

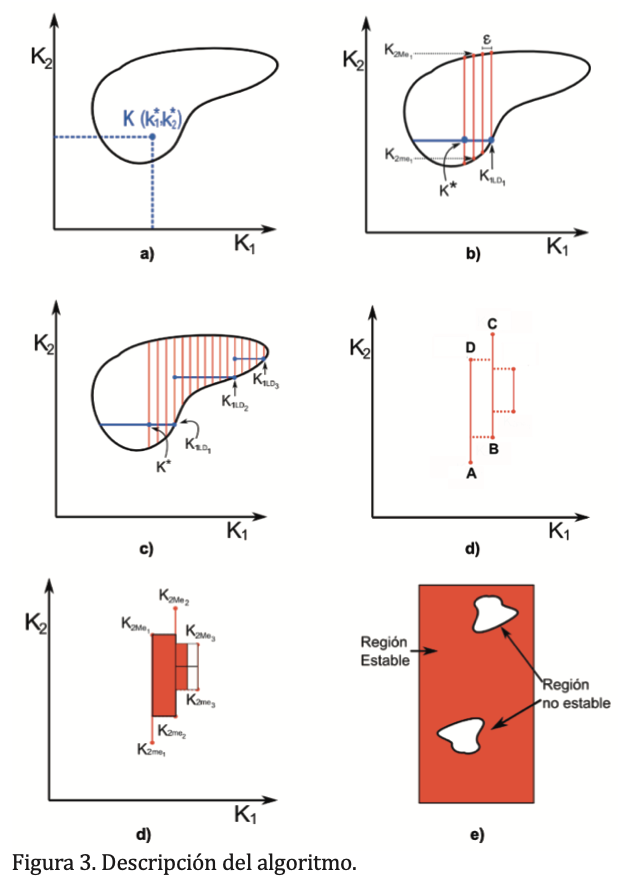
Descripción del algoritmo

El algoritmo hace un análisis de estabilidad robusta en el “punto de partida” para después continuar con la búsqueda de la región en la cual se satisface estabilidad robusta y que se describe a continuación:

 

 

 

 

 

Ejemplo de aplicación

A continuación se muestra un ejemplo de aplicación para el diseño de un controlador robusto. Utilizando la herramienta “descomposición de signo” se prueba la positividad de todas las funciones multivariables polinómicas dela columna σ en el criterio de estabilidad de César Elizondo, descrito anteriormente. Al no haber cambio de signoen la columna σ, es decir, probar que todas las funciones son positivas, se establece una región en el espacio de paramétros del controlador y se comprueba la estabilidad robusta del sistema con incertidumbre paramétrica. Se presenta como ejemplo un motor de inducción, conocido por su robustez, confiabilidad y eficiencia, queademás es objeto de varios trabajos de investigación en diferentes áreas de ingeniería. El modelo dinámico delmotor de inducción puede expresarse y simplificarse como en Chebre, Zerikat y Bendaha (2007), y se puederepresentar mediante el diagrama de bloques mostradoen la figura 3.

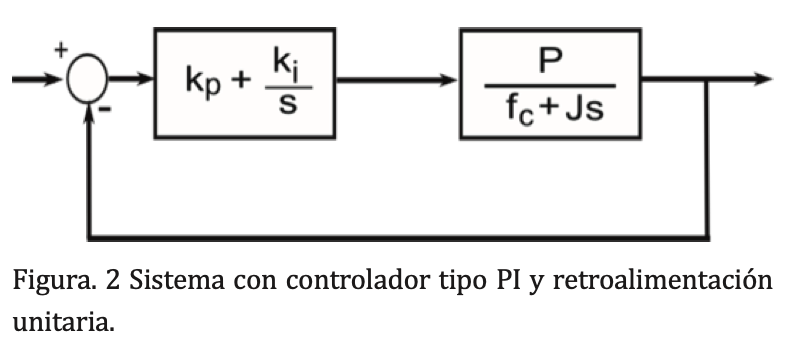
De acuerdo a la nomenclatura de la teoría de control robusta, tenemos las siguientes funciones de transferencia con los siguientes parámetros para el sistema y un controlador tipo PI:

Para este ejemplo se requiere la construcción de un conjunto de controladores que permitan estabilidad robusta, es decir, las raíces reales del polinomio característico en lazo cerrado deben situarse en el semiplano izquierdo del plano complejo.

Se analiza la estabilidad robusta del sistema en lazo cerrado de acuerdo al polinomio característico P(s,q). Por el criterio de estabilidad se obtiene la tabla correspondiente al polinomio y usando la descomposición de signo se analiza positividad robusta de cada uno de los elementos eᵢ.

Los coeficientes de la tabla se presentan a continuación:

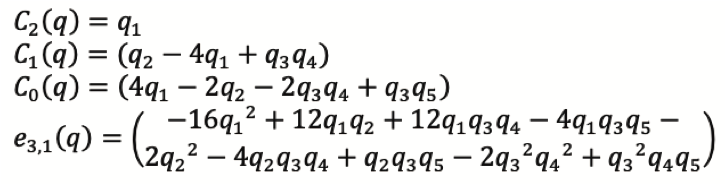
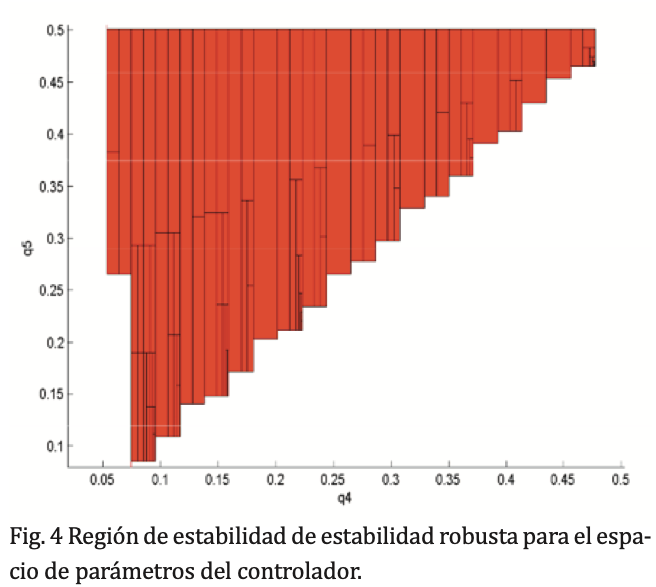
El conjunto de controladores que satisfacen estabilidad robusta al sistema con incertidumbre paramétrica se muestra en la figura 4.

CONCLUSIONES

En este artículo se muestran las diversas herramientas para analizar la positividad robusta de funciones multivariables polinómicas y se da una aplicación en el área de ingeniería de control.

Se propone un enfoque para la construcción de un conjunto de controladores PI mapeando el problema original a un problema de positividad robusta, el cual se resuelve con la herramienta matemática “descomposición de signo”, obteniendo estabilidad robusta de sistemas LTI con incertidumbre paramétrica.

Si el número de parámetros del sistema se incrementa, aumentará también el número de operaciones, y por lo tanto el tiempo en obtener una región de estabilidad. En general, el costo computacional depende del sistema a analizar y la incertidumbre en sus parámetros.

* Universidad Autónoma de Nuevo León.
Contacto: malove1985@gmail.com

REFERENCIAS

Ackermann, J., y Bartlett, A. (1993). Robust Control Systems withUncertain Physical Parameters. Springer. 
Barmish,R.B. (1994).New Tools for Robustness of Linear Systems. New York, NY: Macmillan. 
Bhattacharyya, S.P., Datta, A., y Keel, L.H. (2009). Linear Control Theory, Structure, Robustness and Optimization. Boca Raton,London, New York: Taylor and Francis Group. 
Chebre, M., Zerikat, M., y Bendaha, Y. (2007). Adaptation des Paramétres dé un Contróleur PI par un FLC Appliqué é un Moteur Asynchrone. 4th International Conference on Computer Integrated Manufacturing CIP, 2007, 03-04, Setif, Algeria.
Elizondo, C. (1999). Estabilidad y controlabidad robusta de sistemas lineales con incertidumbre multilineal. Programa Doctoral de la Facultad de Ingeniería Mecánica y Eléctrica de la Universidad Autónoma de Nuevo León. 
Elizondo, C. (2000). Necessary and Su_cient Conditions for Robust Positivity of Polynomic Functions Via Sign Decomposition, Robust Control. Design IFAC ROCOND 2000, Prage Chezc Republic. 
Elizondo, C. (2001). A new stability criterion on space coeficients. Conferences on Decision and Control IEEE. Orlando Florida, USA. 
Elizondo-González, C. (2011). Parametric Robust Stability, Recent Advances in Robust Control Andreas Müller. IntechOpen.DOI: 10.5772/24460. 
Keel, L.H., y Bhattacharyya, S.P. (2008). Fixed Order Multivariable Controller Synthesis: A New Algorithm, Proceedings of the 47th Conference on Decision and Control. Cancún, México. 
Knap, M.J., Keel, L.H., y Bhattacharyya, S.P. (2011). RobustHurwitz stability via sign-definite decomposition. IEEE Transactions on Automatic Control. 56(1). 
Mercader, P., y Banos, A. (2017). A PI tuning rule for integrating plus dead time processes with parametric uncertainty. ISA transactions. 
Mohsenizadeh, D.N., Keel, L.H., y Bhattacharyya, S.P. (2014). An Equivalent Plant Representation for Unknown Control Systems. In: 7th ASME Dynamic Sistems and Control Conference. San Antonio. 
Yedavalli, R.K. (2013). Robust Control of Uncertain Dynamic Systems: A Linear State Space Approach. Springer.